
【题目】抛物线![]() 经过点(1,0),且对称轴为直线
经过点(1,0),且对称轴为直线![]() ,其部分图象如图所示.对于此抛物线有如下四个结论:①
,其部分图象如图所示.对于此抛物线有如下四个结论:①![]() <0; ②
<0; ②![]() ;③9a-3b+c=0;④若
;③9a-3b+c=0;④若![]() ,则
,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值.其中正确结论的序号是( )
时的函数值.其中正确结论的序号是( )
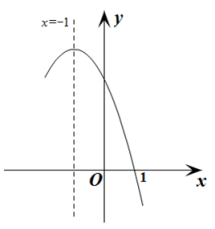
A.①③B.②④C.②③D.③④
【答案】D
【解析】
①根据抛物线开口方向、对称轴、与y轴的交点即可判断;
②根据抛物线的对称轴方程即可判断;
③根据抛物线y=ax2+bx+c经过点(1,0),且对称轴为直线x=﹣1可得抛物线与x轴的另一个交点坐标为(﹣3,0),即可判断;
④根据m>n>0,得出m﹣1和n﹣1的大小及其与﹣1的关系,利用二次函数的性质即可判断.
解:①观察图象可知:
a<0,b<0,c>0,∴abc>0,
所以①错误;
②∵对称轴为直线x=﹣1,
即﹣![]() =﹣1,解得b=2a,即2a﹣b=0,
=﹣1,解得b=2a,即2a﹣b=0,
所以②错误;
③∵抛物线y=ax2+bx+c经过点(1,0),且对称轴为直线x=﹣1,
∴抛物线与x轴的另一个交点为(﹣3,0),
当a=﹣3时,y=0,即9a﹣3b+c=0,
所以③正确;
∵m>n>0,
∴m﹣1>n﹣1>﹣1,
由x>﹣1时,y随x的增大而减小知x=m﹣1时的函数值小于x=n﹣1时的函数值,故④正确;
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
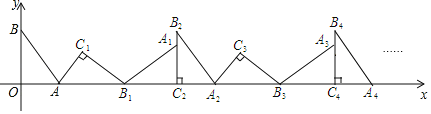
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A(![]() ,0)、B(0,4),则点B2020的横坐标为_____.
,0)、B(0,4),则点B2020的横坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某植物园有一块足够大的空地,其中有一堵长为a米的墙,现准备用20米的篱笆围两间矩形花圃,中间用篱笆隔开.小俊设计了如图甲和乙的两种方案:
方案甲中AD的长不超过墙长;方案乙中AD的长大于墙长.
(1)若a=6.
①按图甲的方案,要围成面积为25平方米的花圃,则AD的长是多少米?
②按图乙的方案,能围成的矩形花圃的最大面积是多少?
(2)若0<a<6.5,哪种方案能围成面积最大的矩形花圃?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
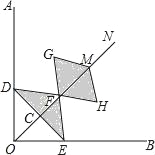
【题目】如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
A. y=![]() B. y=
B. y=![]() C. y=2
C. y=2![]() D. y=3
D. y=3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△BCD中,∠DCB=120°,点E满足∠DEC=60°.
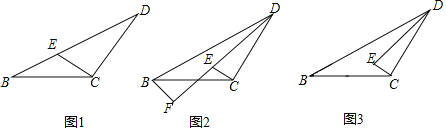
(1)如图1,点E在边BD上时,求证:ED=2BE;
(2)如图2,过点B作DE的垂线交DE的延长线于点F,试探究DE和EF的数量关系,并证明;
(3)若∠DEB=150°,直接写出BE,DE和EC的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70--79分为生产技能良好,60--69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | 75 |
乙 | 78 | 80.5 | 81 |
满意度 | 人数 | 所占百分比 |
非常满意 | 12 |
|
满意 | 54 |
|
比较满意 |
|
|
不满意 | 6 |
|
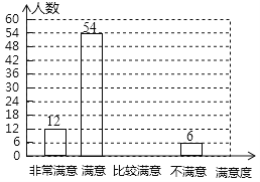
(1)本次调查的总人数为_______.
(2)请补全条形统计图;
(3)据统计,该社区服务站平均每天接待居民约1000名,若将“非常满意”和“消意”作为居民对社区服务站服务工作的肯定,请你估计该社区服务站服务工作平均每天得到多少名居民的肯定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣![]() x2+ax+b交x轴于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是抛物线在第一象限上的一点,过点P作AC的平行线l,分别交直线BC,y轴于点D,点E.
x2+ax+b交x轴于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是抛物线在第一象限上的一点,过点P作AC的平行线l,分别交直线BC,y轴于点D,点E.
(1)填空:直线AC的解析式为 ,抛物线的解析式为 ;
(2)当CD=![]() 时,求OE的长;
时,求OE的长;
(3)当DP=DE时,求点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市每天能出售甲、乙两种肉集装箱共21箱,且甲集装箱3天的销售量与乙集装箱4天的销售量相同.
(1)求甲、乙两种肉类集装箱每天分别能出售多少箱?
(2)若甲种肉类集装箱的进价为每箱200元,乙种肉类集装箱的进价为每箱180元,现超市打算购买甲、乙两种肉类集装箱共100箱,且手头资金不到18080元,则该超市有几种购买方案?
(3)若甲种肉类集装箱的售价为每箱260元,乙种肉类集装箱的售价为每箱230元,在(2)的情况下,哪种方案获利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com