
����Ŀ����֪������y��ax2+��3b+1��x+b��3��a��0����������ʵ��m��ʹ�õ�P��m��m���ڸ��������ϣ����dzƵ�P��m��m��������������ϵ�һ������г������
��1����a��2��b��1ʱ����������ߵ�����г������
��2������������ʵ��b���������Ϻ���������ͬ������г����A��B��
����ʵ��a��ȡֵ��Χ��
������A��B����ֱ��y����x����![]() +1���Գƣ���ʵ��b����Сֵ��
+1���Գƣ���ʵ��b����Сֵ��
���𰸡���1����![]() ����2����2������2����0��a��27��b����Сֵ��
����2����2������2����0��a��27��b����Сֵ��![]()
��������
��1����x=y=m��a=2��b=1���뺯������ʽ���г����̣�ͨ���ⷽ�����m��ֵ���ɣ�
��2���������Ϻ���������ͬ������г����A��B�������m�ķ���m=am2+��3b+1��m+b-3�ĸ����б�ʽ��=9b2-4ab+12a��
����y=9b2-4ab+12a����������ʵ��b������y��0�����Ը��ݶ��κ���y=9b2-4ab+12��ͼ�����ʽ��
�����ö��κ���ͼ��ĶԳ����ʽ�ɣ�
��1����a��2��b��1ʱ��m��2m2+4m+1��4��
���m��![]() ��m����2��
��m����2��
���Ե�P�������ǣ�![]() ��
��![]() ����2����2����
����2����2����
��2��m��am2+��3b+1��m+b��3��
����9b2��4ab+12a��
����y��9b2��4ab+12a����������ʵ��b������y��0��Ҳ����˵������y��9b2��4ab+12��ͼ����b�ᣨ���ᣩ�Ϸ���
���������4a��2��4��9��12a��0��
��0��a��27��
������������������A��x1��y1����B��x2��y2����
��x1��x2��ax2+��3b+1��x+b��3��0��������ʵ����![]() ��
��
���߶�AB���е������ǣ�����![]() ����
����![]() ��������Գ���y��x����
��������Գ���y��x����![]() +1������
+1������
��![]() ��
��![]() ����
����![]() +1����
+1����
��3b+1��![]() +a��
+a��
��a��0��![]() ��0��a
��0��a![]() ��1Ϊ��ֵ��
��1Ϊ��ֵ��
��3b+1��![]() +a��2
+a��2![]() ��2��
��2��
��b��![]() ��
��
��b����Сֵ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
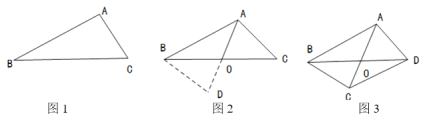
����Ŀ����1��ijѧУ��ѧϰ��ʵ����ѧ��ȤС����������һ����Ŀ����ͼ1����![]() �У���
�У���![]() ���߶�
���߶�![]() �ϣ�
�ϣ�![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �ij���������ѧС���Ա���۷��֣�����
�ij���������ѧС���Ա���۷��֣�����![]() ��
��![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��ͨ������
��ͨ������![]() �Ϳ��Խ�����⣨��ͼ2����ش�
�Ϳ��Խ�����⣨��ͼ2����ش�![]() ��
��![]() ��
��
��2����ο����Ͻ��˼·��������⣺��ͼ![]() ���ı���
���ı���![]() �жԽ���
�жԽ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڰ뾶��4����O�У�AB��CD������ֱ����M��OB���е㣬CM���ӳ��߽���O�ڵ�E����EM��MC������DE��DE=![]() ��
��
��1����֤����AMC�ס�EMB��
��2����EM�ij���
��3����sin��EOB��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���O��б��AB�ϣ���OΪԲ�ģ�OBΪ�뾶��Բ���ֱ���BC��AB�ཻ�ڵ�D��E������AD����֪��CAD����B.
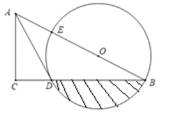
��1����֤��AD�ǡ�O�����ߣ�
��2������B��30����AC��![]() �����ӻ�BD����BD��Χ��Ӱͼ�ε������
�����ӻ�BD����BD��Χ��Ӱͼ�ε������
��3����AC��4��BD��6����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
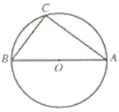
����Ŀ����ͼ����O��ֱ��AB=10����AC=8������BC��
��1���߹���ͼ������CD��ʹCD=BC����D����B�غϣ�������AD����������ͼ�ۼ�����д������
��2���ڣ�1��������ͼ�У����ı���ABCD���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
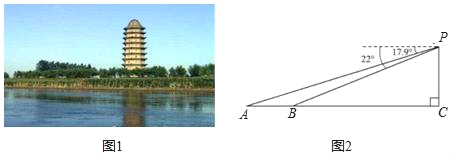
����Ŀ�������������гDZ����˺Ӷ����������������ǡ��˺��Ĵ�������֮һ����ͼ1��.��ѧ��ȤС���С��ͬѧ�����Ϲ۾���P�������ò���Dz���˺������ϵ�A��B����ĸ��Ƿֱ�Ϊ17.9�㣬22�㣬���������C����B�ľ���Ϊ142�ף�A��B��C��ͬһֱ���ϣ���ͼ2�������˺������ϵ�A��B����ľ��루��ȷ��1�ף�.���ο����ݣ�sin22���0.37��cos22���0.93��tan22���0.40��sin17.9���0.31��cos17.9���0.95��tan17.9���0.32��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
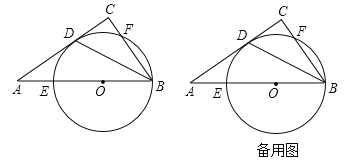
����Ŀ����ͼ����ֱ�ǡ�ABC�У���C��90����AB��5������ABC��ƽ���߽�AC�ڵ�D����AB��ȡ��O���Ե�OΪԲ�ľ���B��D���㻭Բ�ֱ���AB��BC�ཻ�ڵ�E��F�����ڵ�B����
��1����֤��AC�ǡ�O�����ߣ�
��2������Eǡ����AO���е㣬��![]() �ij���
�ij���
��3����CF�ij�Ϊ![]() �������O�İ뾶�����ڵ�F����BD��Գƺ�õ���F�������BFF�����DEF�������֮�ȣ�
�������O�İ뾶�����ڵ�F����BD��Գƺ�õ���F�������BFF�����DEF�������֮�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪A(3��0),B(0��-1)������AB,��B����AB�Ĵ��߶�,ʹBA=BC,����AC.
(1)��ͼ1����C�����ꣻ
(2)��ͼ2,��P���A�����,��x������ƽ��,����BP,������ֱ����������BPQ,����CQ.��֤:PA=CQ.
(3)��(2)��������,��C��P��Q���㹲��,���ʱP�����꼰��APB�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
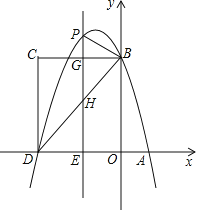
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��x�ύ��A��D���㣬��y�ύ�ڵ�B���ı���OBCD�Ǿ��Σ���A������Ϊ��1��0������B������Ϊ��0��4������֪��E��m��0�����߶�DO�ϵĶ��㣬����E��PE��x�ύ�������ڵ�P����BC�ڵ�G����BD�ڵ�H��
��x�ύ��A��D���㣬��y�ύ�ڵ�B���ı���OBCD�Ǿ��Σ���A������Ϊ��1��0������B������Ϊ��0��4������֪��E��m��0�����߶�DO�ϵĶ��㣬����E��PE��x�ύ�������ڵ�P����BC�ڵ�G����BD�ڵ�H��
��1����������ߵĽ���ʽ��
��2������P��ֱ��BC�Ϸ�ʱ�����ú�m�Ĵ���ʽ��ʾPG�ij��ȣ�
��3���ڣ�2���������£��Ƿ���������ĵ�P��ʹ����P��B��GΪ���������������DEH���ƣ������ڣ������ʱm��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com