
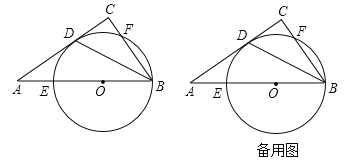
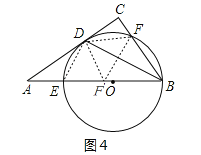
【题目】如图,在直角△ABC中,∠C=90°,AB=5,作∠ABC的平分线交AC于点D,在AB上取点O,以点O为圆心经过B、D两点画圆分别与AB、BC相交于点E、F(异于点B).
(1)求证:AC是⊙O的切线;
(2)若点E恰好是AO的中点,求![]() 的长;
的长;
(3)若CF的长为![]() ,①求⊙O的半径长;②点F关于BD轴对称后得到点F′,求△BFF′与△DEF′的面积之比.
,①求⊙O的半径长;②点F关于BD轴对称后得到点F′,求△BFF′与△DEF′的面积之比.
【答案】(1)见解析;(2)![]() ;(3)①r1=1,
;(3)①r1=1,![]() ;②△BFF'与△DEF'的面积比为
;②△BFF'与△DEF'的面积比为![]() 或
或![]()
【解析】
(1)连结![]() ,证明
,证明![]() ,得出
,得出![]() ,则结论得证;
,则结论得证;
(2)求出![]() ,
,![]() ,连结
,连结![]() ,则
,则![]() ,由弧长公式可得出答案;
,由弧长公式可得出答案;
(3)①如图3,过![]() 作
作![]() 于
于![]() ,则
,则![]() ,四边形
,四边形![]() 是矩形,设圆的半径为
是矩形,设圆的半径为![]() ,则
,则![]() .
.![]() ,证明
,证明![]() ,由比例线段可得出
,由比例线段可得出![]() 的方程,解方程即可得出答案;
的方程,解方程即可得出答案;
②证明![]() ,当
,当![]() 或
或![]() 时,根据相似三角形的性质可得出答案.
时,根据相似三角形的性质可得出答案.
解:(1)连结DO,
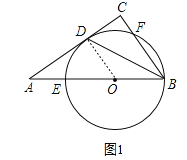
∵BD平分∠ABC,
∴∠CBD=∠ABD,
∵DO=BO,
∴∠ODB=∠OBD,
∴∠CBD=∠ODB.
∴DO∥BC,
∵∠C=90°,
∴∠ADO=90°,
∴AC是⊙O的切线;
(2)∵E是AO中点,
∴AE=EO=DO=BO=![]() ,
,
∴sin∠A=![]() ,
,
∴∠A=30°,∠B=60°,
连结FO,则∠BOF=60°,
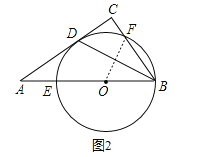
∴![]() =
=![]() .
.
(3)①如图3,连结OD,过O作OM⊥BC于M,
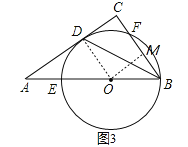
则BM=FM,四边形CDOM是矩形
设圆的半径为r,则OA=5﹣r.BM=FM=r﹣![]() ,
,
∵DO∥BC,
∴∠AOD=∠OBM,
而∠ADO=90°=∠OMB,
∴△ADO∽△OMB,
∴![]() ,
,
即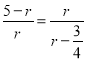 ,
,
解之得r1=1,![]() .
.
②∵在(1)中∠CBD=∠ABD,
∴DE=DF,
∵BE是⊙O的直径,
∴∠BDE=90°,
而F、F'关于BD轴对称,
∴BD⊥FF',BF=BF',
∴DE∥FF',
∴∠DEF'=∠BF'F,
∴△DEF'∽∠BFF',
当r=1时,AO=4,DO=1,BO=1,
由①知![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
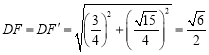 ,
,
![]() 与
与![]() 的面积之比
的面积之比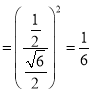 ,
,
同理可得,当![]() 时.时,
时.时,![]() 与
与![]() 的面积比
的面积比![]() .
.
![]() 与
与![]() 的面积比为
的面积比为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
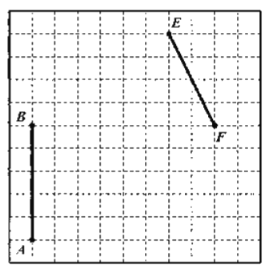
【题目】如图为正方形网格,每个小正方形的边长均为1,各个小正方形的顶点叫做格点,请在下面的网格中按要求分别画图,使得每个图形的顶点均在格点上.
(1)在图中画一个以![]() 为一边的菱形
为一边的菱形![]() ,且菱形
,且菱形![]() 的面积等于20.
的面积等于20.
(2)在图中画一个以![]() 为对角线的正方形
为对角线的正方形![]() ,并直接写出正方形
,并直接写出正方形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC与△ABD中,∠CAB=∠DBA=β,且∠ADB+∠ACB=180°.

提出问题:如图1,当∠ADB=∠ACB=90°时,求证:AD=BC;
类比探究:如图2,当∠ADB≠∠ACB时,AD=BC是否还成立?并说明理由.
综合运用:如图3,当β=18°,BC=1,且AB⊥BC时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+(3b+1)x+b﹣3(a>0),若存在实数m,使得点P(m,m)在该抛物线上,我们称点P(m,m)是这个抛物线上的一个“和谐点”.
(1)当a=2,b=1时,求该抛物线的“和谐点”;
(2)若对于任意实数b,抛物线上恒有两个不同的“和谐点”A、B.
①求实数a的取值范围;
②若点A,B关于直线y=﹣x﹣(![]() +1)对称,求实数b的最小值.
+1)对称,求实数b的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
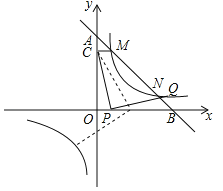
【题目】如图,一次函数![]() (
(![]() )的图象与坐标轴交于A,B两点,与反比例函数
)的图象与坐标轴交于A,B两点,与反比例函数![]() (
(![]() )的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.
)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.
(1)求![]() 的值;
的值;
(2)若![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)在(2)的条件下,设点P是x轴(除原点O外)上一点,将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出所有的点Q的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
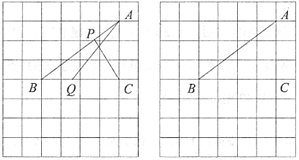
【题目】如图,在由边长都为1的小正方形组成的网格中,点![]() ,
,![]() ,
,![]() 均为格点,点
均为格点,点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点,且满足
上的动点,且满足![]() .
.
(1)线段![]() 的长度等于__________;
的长度等于__________;
(2)当线段![]() 取得最小值时,请借助无刻度直尺在给定的网格中画出线段
取得最小值时,请借助无刻度直尺在给定的网格中画出线段![]() 和
和![]() ,并简要说明你是怎么画出点Q,P的:_______________________.
,并简要说明你是怎么画出点Q,P的:_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
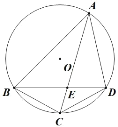
【题目】已知:如图,四边形 ABCD 内接于⊙ O ,AC 和 BD 相交于E , BC = CD = 4 , AE = 6 ,且 BE 和 DE 的长是正整数,求 BD 的 长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com