
【题目】已知:△ABC与△ABD中,∠CAB=∠DBA=β,且∠ADB+∠ACB=180°.

提出问题:如图1,当∠ADB=∠ACB=90°时,求证:AD=BC;
类比探究:如图2,当∠ADB≠∠ACB时,AD=BC是否还成立?并说明理由.
综合运用:如图3,当β=18°,BC=1,且AB⊥BC时,求AC的长.
【答案】(1)见解析;(2)仍然成立,理由见解析;(3)![]() +1
+1
【解析】
(1)证明△DBA≌△CAB即可;
(2)作∠BEC=∠BCE,BE交AC于E,证明△DBA≌△EAB即可;
(3)作∠BEC=∠BCE,BE交AC于E,由(2)得,AD=BC=BE=1,通过角之间的关系可求得EF=BE=1,再证△CBE∽△CFB,根据相似三角形的对应边成比例求解即可.
(1)在△BDA和△CAB中
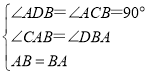
∴△DBA≌△CAB(AAS);
(2)结论仍然成立.
理由:作∠BEC=∠BCE,BE交AC于E.
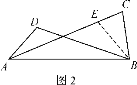
∵∠ADB+∠ACB=∠AEB+∠BEC=180°
∴∠ADB=∠AEB.
又∠CAB=∠DBA,AB=BA
∴△DBA≌△EAB(AAS),
∴BE=AD,
∵∠BEC=∠BCE,
∴BC=BE,
∴AD=BC.
(3)作∠BEC=∠BCE,BE交AC于E,
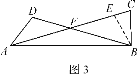
由(2)得,AD=BC=BE=1
在Rt△ACB中,∠CAB=18°
∴∠C=72°,∠BEC=∠C= 72°
由∠CFB=∠CAB+∠DBA=36°
∴∠EBF=∠CEB-∠CFB=36°
∴EF=BE=1
在△BCF中,∠FBC=180°-∠BFC-∠C=72°
∴∠FBC=∠BEC,∠C=∠C
∴△CBE∽△CFB
∴![]() =
=![]()
令CE=x,∴1=x(x+1)
解之,x=![]()
∴CF=![]()
由∠FBC=∠BEC
∴BF=CF.又AF=BF
∴AC=2CF=![]() +1
+1


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象过点
的图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,给出以下结论:①
,给出以下结论:①![]() ;②
;②![]() ;③
;③![]() :④若
:④若![]() 为函数图象上的两点,则
为函数图象上的两点,则![]() .其中正确的是( )
.其中正确的是( )
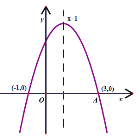
A.①②④B.①②③C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“过直线外一点作已知直线的平行线”的尺规作图过程.
已知:直线![]() 及直线
及直线![]() 外一点P.
外一点P.

求作:直线![]() ,使
,使![]() .
.
作法:如图,

①在直线![]() 上取一点O,以点O为圆心,
上取一点O,以点O为圆心,![]() 长为半径画半圆,交直线
长为半径画半圆,交直线![]() 于
于![]() 两点;
两点;
②连接![]() ,以B为圆心,
,以B为圆心,![]() 长为半径画弧,交半圆于点Q;
长为半径画弧,交半圆于点Q;
③作直线![]() .
.
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据小明设计的尺规作图过程:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明
证明:连接![]() ,
,
∵![]() ,
,
∴![]() __________.
__________.
∴![]() (______________)(填推理的依据).
(______________)(填推理的依据).
∴![]() (_____________)(填推理的依据).
(_____________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了在七年级600名学生中顺利开展“四点半”课堂,采用随机抽样的方法,从喜欢乒乓球、跳绳、篮球、绘画四个方面调查了若干名学生,并绘制了条形统计图和扇形统计图,请结合两幅统计图,回答下列问题:
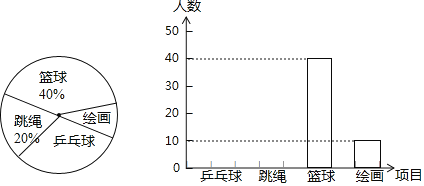
(1)这次调查活动中,一共调查了 名学生;
(2)“乒乓球”所在扇形的圆心角是 度;
(3)请补全条形统计图;
(4)根据本次调查情况,请你估计七年级600名学生中喜欢“乒乓球”的人数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() ).
).
(1)求出二次函数图象的对称轴;
(2)若该二次函数的图象经过点![]() ,且整数
,且整数![]() ,
,![]() 满足
满足![]() ,求二次函数的表达式;
,求二次函数的表达式;
(3)对于该二次函数图象上的两点![]() ,
,![]() ,设
,设![]() ,当
,当![]() 时,均有
时,均有![]() ,请结合图象,直接写出
,请结合图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?(不要求说明理由)
频率分布表 | ||
分组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 8 | 0.16 |
70.5~80.5 | 10 | 0.20 |
80.5~90.5 | 16 | 0.32 |
90.5~100.5 | ||
合计 | ||

查看答案和解析>>
科目:初中数学 来源: 题型:
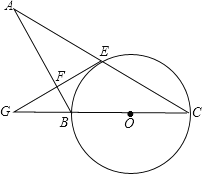
【题目】如图,AB=BC,以BC为直径作⊙O,AC交⊙O于点E,过点E作EG⊥AB于点F,交CB的延长线于点G.
(1)求证:EG是⊙O的切线;
(2)若GF=2![]() ,GB=4,求⊙O的半径.
,GB=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】远远在一个不透明的盒子里装了4个除颜色外其他都相同的小球,其中有3个是红球,1个是绿球,每次拿一个球然后放回去,拿2次,则至少有一次取到绿球的概率是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com