
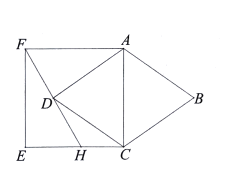
【题目】如图,以菱形![]() 的对角线
的对角线![]() 为边,在
为边,在![]() 的左侧作正方形
的左侧作正方形![]() 连结
连结![]() 并延长交
并延长交![]() 于点
于点![]() .若正方形
.若正方形![]() 的面积是菱形
的面积是菱形![]() 面积的
面积的![]() 倍,
倍,![]() ,则
,则![]() _________________.
_________________.
【答案】![]()
【解析】
连接BD交AC于G,由菱形性质可得AC与BD互相垂直平分,菱形面积等于AC与BD的积的一半,可得S菱形ABCD=ACDG,因为G是AC中点且DG∥EC∥AF,根据平行线分线段成比例定理可知点D也是FH中点,故DG是梯形ACHF中位线,DG=![]() (CH+AF)=
(CH+AF)=![]() (CH+EF),因此菱形ABCD面积可用含EF的式子表示,然后以正方形面积为菱形面积的1.4倍为等量关系列方程,即可求出EF的长.
(CH+EF),因此菱形ABCD面积可用含EF的式子表示,然后以正方形面积为菱形面积的1.4倍为等量关系列方程,即可求出EF的长.
解:连接BD,交AC于点G,
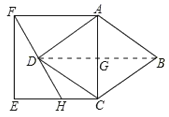
∵四边形ABCD是菱形,
∴AC⊥BD,DB=2DG,AG=CG,
∴S菱形ABCD=![]() ACDB=ACDG,
ACDB=ACDG,
∵四边形ACEF是正方形,
∴EF=AF=AC=CE,AF∥EC,AC⊥EC,
∴DB∥CE∥AF,
∴![]() ,即DG为梯形ACHF的中位线,
,即DG为梯形ACHF的中位线,
∴DG=![]() (CH+AF)=
(CH+AF)=![]() (CH+EF),
(CH+EF),
∵CH=6,正方形![]() 的面积是菱形
的面积是菱形![]() 面积的
面积的![]() 倍,
倍,
∴EF2=1.4ACDG,
∴EF2=1.4EF·![]() (6+EF),
(6+EF),
∴EF=14,
故答案为:14.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
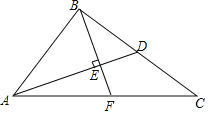
【题目】如图,在Rt△ACB中,∠ABC=90°,D为BC边的中点,BE⊥AD于点E,交AC于F,若AB=4,BC=6,则线段EF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是![]() 的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转
的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转![]() 得到线段
得到线段![]() .射线
.射线![]() 与
与![]() 交于点Q.已知
交于点Q.已知![]() ,设P,C两点间的距离为xcm,P,D两点间的距离
,设P,C两点间的距离为xcm,P,D两点间的距离![]() ,P,Q两点的距离为
,P,Q两点的距离为![]() .
.
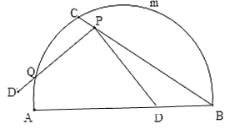
小石根据学习函数的经验,分别对函数![]() ,
,![]() ,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() ,与x的几组对应值:
,与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.0 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数据所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
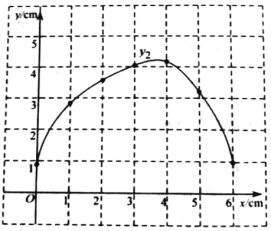
(3)结合函数图象,解决问题:连接DQ,当△DPQ为等腰三角形时,PC的长度约为_____cm.(结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
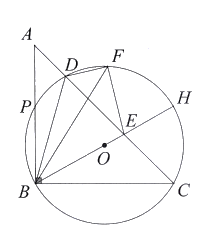
【题目】如图,在![]() 中,
中,![]() (圆心
(圆心![]() 在
在![]() 内部)经过
内部)经过![]() 两点,交线段
两点,交线段![]() 于点
于点![]() 直径
直径![]() 交
交![]() 于点
于点![]() 点
点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 落在
落在![]() 上.连结
上.连结![]() .
.
![]() 求证:
求证:![]() .
.
![]() 在圆心
在圆心![]() 的运动过程中,
的运动过程中,
![]() 若
若![]() ,求
,求![]() 的长.
的长.
![]() 若点
若点![]() 关于
关于![]() 的对称点落在
的对称点落在![]() 边上时,求
边上时,求![]() 的值.(直接写出答案)
的值.(直接写出答案)
![]() 令
令![]() 与边
与边![]() 的另一个交点为
的另一个交点为![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() 若
若![]() ,垂足为点
,垂足为点![]() 求证:
求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC与△ABD中,∠CAB=∠DBA=β,且∠ADB+∠ACB=180°.

提出问题:如图1,当∠ADB=∠ACB=90°时,求证:AD=BC;
类比探究:如图2,当∠ADB≠∠ACB时,AD=BC是否还成立?并说明理由.
综合运用:如图3,当β=18°,BC=1,且AB⊥BC时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月23日为世界阅读日,为响应党中央“倡导全民阅读,建设书香会”的号召,某校团委组织了一次全校学生参加的“读书活动”大赛为了解本次赛的成绩,校团委随机抽取了部分学生的成绩(成绩![]() 取整数,总分100分)作为本进行统计,制成如下不完整的统计图表(频数频率分布表和频数分布直方图):
取整数,总分100分)作为本进行统计,制成如下不完整的统计图表(频数频率分布表和频数分布直方图):
成绩 | 频数(人) | 频率 |
| 10 | 0.05 |
| 30 | 0.15 |
| 40 |
|
|
| 0.35 |
| 50 | 0.25 |
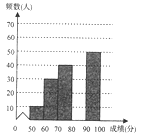
根据所给信息,解答下列问题:
(1)抽取的样本容量是 ;![]() ,
,![]() ;
;
(2)补全频数分布直方图;这200名学生成绩的中位数会落在 分数段;
(3)全校有1200名学生参加比赛,若得分为90分及以上为优秀,请你估计全校参加比赛成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
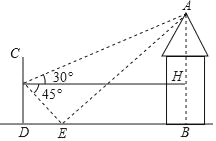
【题目】为了测量休闲凉亭AB的高度,某数学兴趣小组在水平地面D处竖直放置一个标杆CD,并在地面上水平放置一个平面镜E,使得B、E、D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到凉亭顶端A,在F处测得凉亭A顶端的仰角为30°,平面镜E的俯角为45°,FD=2米,求休闲凉亭AB的高度.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com