
����Ŀ����ͼ��һ�κ���![]() ��
��![]() ����ͼ���������ύ��A��B���㣬�뷴��������
����ͼ���������ύ��A��B���㣬�뷴��������![]() ��
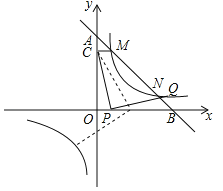
��![]() ����ͼ����M��N���㣬����M��MC��y���ڵ�C����֪CM=1��
����ͼ����M��N���㣬����M��MC��y���ڵ�C����֪CM=1��
��1����![]() ��ֵ��
��ֵ��
��2����![]() �����������Ľ���ʽ��
�����������Ľ���ʽ��
��3���ڣ�2���������£����P��x�ᣨ��ԭ��O�⣩��һ�㣬���߶�CP�Ƶ�P��˳ʱ�����ʱ����ת90��õ��߶�PQ������P����ʱ����Q�ܷ��ڷ�����������ͼ���ϣ�����ܣ�������еĵ�Q�����ꣻ������ܣ���˵�����ɣ�
���𰸡���1��5����2��![]() ����3����Q������Ϊ��2+
����3����Q��������2+![]() ����2+
����2+![]() ����2��
����2��![]() ����2��
����2��![]() ����2����2����
����2����2����
��������
��1�����ݵ�M��������뷴������ϵ��![]() �У��ɵý��ۣ�
�У��ɵý��ۣ�
��2�����ݡ�ACM�ס�ADN����![]() ����CM=1��DN=4��ͬ����N�����꣬���뷴��������ʽ�пɵ�k2��ֵ��
����CM=1��DN=4��ͬ����N�����꣬���뷴��������ʽ�пɵ�k2��ֵ��
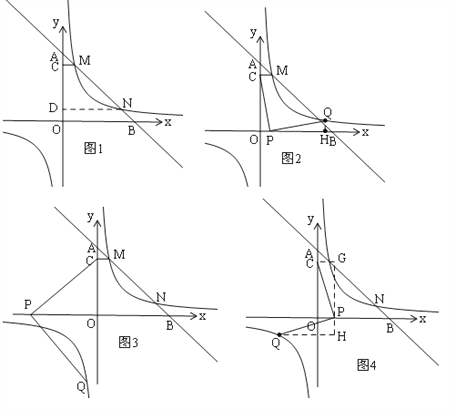
��3����ͼ2����P��x�����������ʱ����P˳ʱ����ת����Q�����ݡ�COP�ա�PHQ����CO=PH��OP=QH����P��x��0������ʾQ��x+4��x�������뷴���������Ĺ�ϵʽ�пɵ�Q���������ꣻ
��ͼ3����P��x��ĸ�������ʱ��
��ͼ4����P��x�����������ʱ����P��ʱ����ת����Q��ͬ���ɵý��ۣ�
�⣺��1����ͼ1��
��MC��y���ڵ�C����CM=1��
��M�ĺ�����Ϊ1����x=1ʱ��y=k1+5��
��M��1��k1+5����
��M�ڷ�����������ͼ���ϣ�
��1����k1+5��=k2��
��k2��k1=5��
��2����ͼ1����N��ND��y����D��
��CM��DN��
���ACM�ס�ADN��
��![]() ��
��
��CM=1��
��DN=4����x=4ʱ��y=4k1+5��
��N��4��4k1+5����
��4��4k1+5��=k2�٣�
�ɣ�1���ã�k2��k1=5��
��k1=k2��5�ڣ�
�Ѣڴ���ٵã�4��4k2��20+5��=k2��k2=4��
�෴���������Ľ���ʽ��![]() ��
��
��3������P����ʱ����Q���ڷ�����������ͼ���ϣ�
��ͼ2��CP=PQ����CPQ=90�㣬��Q��QH��x����H��
�ã���COP�ա�PHQ��
��CO=PH��OP=QH��
�ɣ�2��֪�������������Ľ���ʽ��![]() ��
��
��x=1ʱ��y=4��
��M��1��4����
��OC=PH=4��
��P��x��0����
��Q��x+4��x����
����Q���ڷ�����������ͼ����ʱ��x��x+4��=4��x2+4x+4=8��x=��2��![]() ��
��
��x=��2+![]() ʱ��x+4=2+
ʱ��x+4=2+![]() ��
��
��ͼ2��Q��2+![]() ����2+
����2+![]() ����
����
��x=��2��![]() ʱ��x+4=2��
ʱ��x+4=2��![]() ����ͼ3��Q��2��
����ͼ3��Q��2��![]() ����2��
����2��![]() ����
����
��ͼ4��CP=PQ����CPQ=90�㣬
��P��x��0������P��GH��y�ᣬ��C��CG��GH����Q��QH��GH���ã���CPG�ա�PQH��
��PG=QH=4��CG=PH=x��
��Q��x��4����x����
ͬ���ã���x��x��4��=4����ã�x1=x2=2��
��Q����2����2����
������������Q��������2+![]() ����2+
����2+![]() ����2��
����2��![]() ����2��
����2��![]() ����2����2����
����2����2����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����![]() �Ķ���
�Ķ���![]() ��
��![]() ���ϣ�
���ϣ�![]() ��
��![]() ���ϣ��Ѿ���
���ϣ��Ѿ���![]() �ضԽ���
�ضԽ���![]() ���ڵ�ֱ�߶��ۣ���
���ڵ�ֱ�߶��ۣ���![]() ǡ�����ڷ���������
ǡ�����ڷ���������![]() ��ͼ���ϵ�
��ͼ���ϵ�![]() ����
����![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ���ӳ�
���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() �պ���
�պ���![]() ���е�.��֪
���е�.��֪![]() ������Ϊ
������Ϊ![]() ��
��
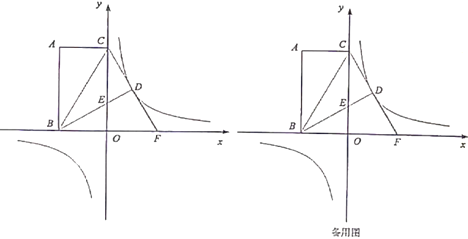
��1����������![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2����![]() �Ƿ���������
�Ƿ���������![]() ͼ���ϵ�һ�㣬
ͼ���ϵ�һ�㣬![]() ����
����![]() ���ϣ�����
���ϣ�����![]() Ϊ������ı�����ƽ���ı��Σ���ֱ��д��
Ϊ������ı�����ƽ���ı��Σ���ֱ��д��![]() �������_________.
�������_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ֱ��������ֽƬABC����ACB��90����AB��10��AC��6����DΪBC���ϵ���һ�㣬�ع���D��ֱ���۵���ʹֱ�Ƕ���C����б��AB�ϵĵ�E��������BDE��ֱ��������ʱ����CD�ij�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��AB=10����AC=8������BC��
��1���߹���ͼ������CD��ʹCD=BC����D����B�غϣ�������AD����������ͼ�ۼ�����д������
��2���ڣ�1��������ͼ�У����ı���ABCD���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
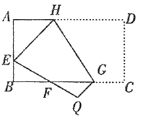
����Ŀ����ͼ��������![]() ��
��![]() ���ۣ���
���ۣ���![]() ����
����![]() ������
������![]() ����
����![]() ���ϵ�
���ϵ�![]() ����
����![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ����
����![]() �ܳ��Ĵ�СΪ_________��
�ܳ��Ĵ�СΪ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
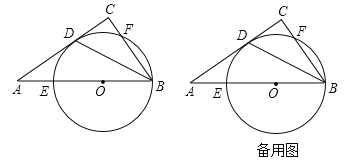
����Ŀ����ͼ����ֱ�ǡ�ABC�У���C��90����AB��5������ABC��ƽ���߽�AC�ڵ�D����AB��ȡ��O���Ե�OΪԲ�ľ���B��D���㻭Բ�ֱ���AB��BC�ཻ�ڵ�E��F�����ڵ�B����
��1����֤��AC�ǡ�O�����ߣ�
��2������Eǡ����AO���е㣬��![]() �ij���
�ij���
��3����CF�ij�Ϊ![]() �������O�İ뾶�����ڵ�F����BD��Գƺ�õ���F�������BFF�����DEF�������֮�ȣ�
�������O�İ뾶�����ڵ�F����BD��Գƺ�õ���F�������BFF�����DEF�������֮�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ϊ�˴���ʡ�������سǣ�ȫ��������СѧУ�����������ļ�ֵ���������ã�ijУ��ȫУѧ�������˼�����ۣ��������Ϊ![]() (����)��
(����)��![]() (����)��
(����)��![]() (�ϸ�)��
(�ϸ�)��![]() (���ϸ�)�ĸ��ȼ����������ȡ������ѧ���ļ������Ϊ�����������ݴ�����������������ʾ��������ͳ�Ʊ���ͳ��ͼ��
(���ϸ�)�ĸ��ȼ����������ȡ������ѧ���ļ������Ϊ�����������ݴ�����������������ʾ��������ͳ�Ʊ���ͳ��ͼ��
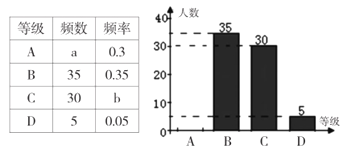
�����ͳ�Ʊ���ͳ��ͼ�ṩ����Ϣ������������⣺
��1�����������ȡ����������Ϊ__________��
��2��ͳ�Ʊ���![]() _________��
_________��![]() _________��
_________��
��3������У����ѧ��5000�ˣ���������Уѧ���ڱ��μ���дﵽ��![]() (����)���ȼ���ѧ��������
(����)���ȼ���ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��
��
��1�������꣬�Գ��
��2��![]() ȡ��ֵʱ��
ȡ��ֵʱ�� ![]() ��
��![]() �����������
�����������
��3��![]() ȡ��ֵʱ��
ȡ��ֵʱ�� ![]() ��0��
��0�� ![]() ȡ��ֵʱ��
ȡ��ֵʱ�� ![]() ��0��
��0�� ![]() ȡ��ֵʱ��
ȡ��ֵʱ�� ![]() ��0 ��
��0 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺����������ʵ��a��b����![]() ��0������
��0������![]() ��0��
��0��
��![]() ��
��![]() ��ֻ�е�a��bʱ���Ⱥų�����
��ֻ�е�a��bʱ���Ⱥų�����
���ۣ���![]() ��
��![]() ��a��b��Ϊ��ʵ�����У���abΪ��ֵp����a+b��
��a��b��Ϊ��ʵ�����У���abΪ��ֵp����a+b��![]() ��ֻ�е�a��bʱ��a+b����Сֵ
��ֻ�е�a��bʱ��a+b����Сֵ![]() ��
��
�����������ݣ��ش��������⣺
��m��0��ֻ�е�m�� ʱ��![]() ����Сֵ ��
����Сֵ ��
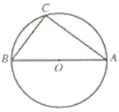
˼����֤����ͼ1��ABΪ��ԲO��ֱ����CΪ��Բ������һ�㣨���A��B���غϣ�������C��CD��AB������ΪD��AD��a��DB��b��
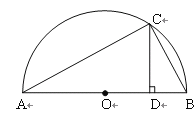
�Ը���ͼ����֤![]() ��
��![]() ����ָ���Ⱥų���ʱ��������
����ָ���Ⱥų���ʱ��������
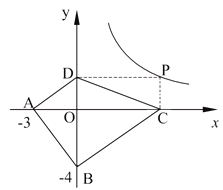
̽��Ӧ�ã���ͼ2����֪A(��3��0)��B(0����4)��PΪ˫����![]() ��x��0���ϵ�����һ�㣬����P��PC��x���ڵ�C��PD��y���ڵ�D�����ı���ABCD�������Сֵ����˵����ʱ�ı���ABCD����״��
��x��0���ϵ�����һ�㣬����P��PC��x���ڵ�C��PD��y���ڵ�D�����ı���ABCD�������Сֵ����˵����ʱ�ı���ABCD����״��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com