
【题目】今年我县为了创建省级文明县城,全面推行中小学校“社会主义核心价值观”进课堂.某校对全校学生进行了检测评价,检测结果分为![]() (优秀)、
(优秀)、![]() (良好)、
(良好)、![]() (合格)、
(合格)、![]() (不合格)四个等级.并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如下所示不完整的统计表和统计图.
(不合格)四个等级.并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如下所示不完整的统计表和统计图.
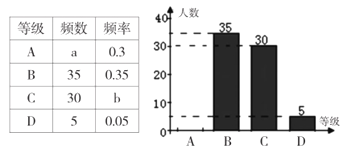
请根据统计表和统计图提供的信息,解答下列问题:
(1)本次随机抽取的样本容量为__________;
(2)统计表中![]() _________,
_________,![]() _________.
_________.
(3)若该校共有学生5000人,请你估算该校学生在本次检测中达到“![]() (优秀)”等级的学生人数.
(优秀)”等级的学生人数.
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】(1)在浙江卫视全新推出的大型户外竞技真人秀节目﹣﹣《奔跑吧兄弟》中,七位主持人邓超、王祖蓝、王宝强、李晨、陈赫、郑凯及Angelababy(杨颖)在“撕名牌环节”的成绩分别为:8,5,7,8,6,8,5,则这组数据的众数和中位数分别是 .
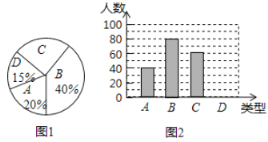
(2)某学校想了解学生对撕名牌游戏的喜欢程度,对学校部分学生进行了抽样调查,就学生对游戏的喜欢程度(A:喜欢;B:一般;C:不喜欢;D:无所谓)进行数据统计,并绘制了如下两幅不完整的统计图.
①此次调查的样本容量为 ;
②条形统计图中存在的错误是 (填A、B、C中的一个);
③在图2中补画条形统计图中不完整的部分;
④若从该校喜欢撕名牌游戏的学生中抽取10人进行比赛,则喜欢撕名牌游戏的小明被抽中的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
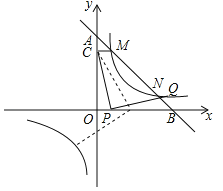
【题目】如图,一次函数![]() (
(![]() )的图象与坐标轴交于A,B两点,与反比例函数
)的图象与坐标轴交于A,B两点,与反比例函数![]() (
(![]() )的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.
)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.
(1)求![]() 的值;
的值;
(2)若![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)在(2)的条件下,设点P是x轴(除原点O外)上一点,将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出所有的点Q的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图 1,若 P是口ABCD 边 CD 上任意一点,连结 AP、BP,若△APB 的面积为 60 ,△APD 的面积为 18,则 S△APC= .
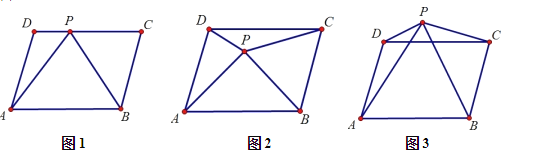
(2) 如图 2,①若点 P 运动到口ABCD 内一点时,试说明 S△APB +S△DPC =S△BPC +S△APD.
②若此时△APB 的面积为 60,△APD 的面积为 18,则 S△APC= .
(3)如图 3①利用(2)中的方法你会发现,S△APB ,S△DPC ,S△BPC ,S△APD 之间存在怎样的关系: .
②若此时△APB 的面积为 60,△APD 的面积为 18,请利用你的发现,求 S△APC 的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
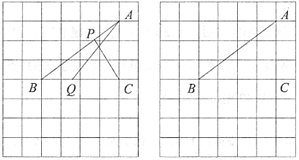
【题目】如图,在由边长都为1的小正方形组成的网格中,点![]() ,
,![]() ,
,![]() 均为格点,点
均为格点,点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点,且满足
上的动点,且满足![]() .
.
(1)线段![]() 的长度等于__________;
的长度等于__________;
(2)当线段![]() 取得最小值时,请借助无刻度直尺在给定的网格中画出线段
取得最小值时,请借助无刻度直尺在给定的网格中画出线段![]() 和
和![]() ,并简要说明你是怎么画出点Q,P的:_______________________.
,并简要说明你是怎么画出点Q,P的:_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
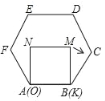
【题目】已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示:按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转……连续经过六次旋转.在旋转的过程中,当正方形和正六边形的边重合时,点B,M间的距离可能是( )
A. 0.5B. 0.7C. ![]() ﹣1D.
﹣1D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上的一点,连接BO交AD于点F,OE⊥OB交BC边于点E.
(1)试说明:△ABF∽△COE.
(2)如图(2),当O为AC边的中点,且![]() 时,求
时,求![]() 的值.
的值.
(3)当O为AC边的中点,![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com