
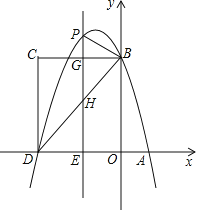
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)PG=
;(2)PG=![]() ;(3)存在点P,使得以P、B、G为顶点的三角形与△DEH相似,此时m的值为﹣1或
;(3)存在点P,使得以P、B、G为顶点的三角形与△DEH相似,此时m的值为﹣1或![]() .
.
【解析】
试题(1)将A(1,0),B(0,4)代入![]() ,运用待定系数法即可求出抛物线的解析式.
,运用待定系数法即可求出抛物线的解析式.
(2)由E(m,0),B(0,4),得出P(m,![]() ),G(m,4),则由
),G(m,4),则由![]() 可用含m的代数式表示PG的长度.
可用含m的代数式表示PG的长度.
(3)先由抛物线的解析式求出D(﹣3,0),则当点P在直线BC上方时,﹣3<m<0.分两种情况进行讨论:①△BGP∽△DEH;②△PGB∽△DEH.都可以根据相似三角形对应边成比例列出比例关系式,进而求出m的值.
试题解析:解:(1)∵抛物线![]() 与x轴交于点A(1,0),与y轴交于点B(0,4),
与x轴交于点A(1,0),与y轴交于点B(0,4),
∴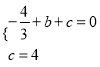 ,解得
,解得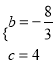 .
.
∴抛物线的解析式为![]() .
.
(2)∵E(m,0),B(0,4),PE⊥x轴交抛物线于点P,交BC于点G,
∴P(m,![]() ),G(m,4).
),G(m,4).
∴PG=![]() .
.
(3)在(2)的条件下,存在点P,使得以P、B、G为顶点的三角形与△DEH相似.
∵![]() ,∴当y=0时,
,∴当y=0时,![]() ,解得x=1或﹣3.
,解得x=1或﹣3.
∴D(﹣3,0).
当点P在直线BC上方时,﹣3<m<0.
设直线BD的解析式为y=kx+4,
将D(﹣3,0)代入,得﹣3k+4=0,解得k=![]() .
.
∴直线BD的解析式为y=![]() x+4. ∴H(m,
x+4. ∴H(m,![]() m+4).
m+4).
分两种情况:
①如果△BGP∽△DEH,那么![]() ,即
,即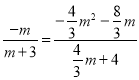 .
.
由﹣3<m<0,解得m=﹣1.
②如果△PGB∽△DEH,那么![]() ,即
,即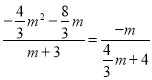 .
.
由﹣3<m<0,解得m=![]() .
.
综上所述,在(2)的条件下,存在点P,使得以P、B、G为顶点的三角形与△DEH相似,此时m的值为﹣1或![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
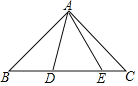
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°
(1)若BD=2,CE=4,则DE=_____.
(2)若∠AEB=75°,则线段BD与CE的数量关系是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
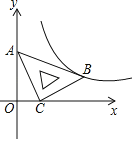
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
A.(![]() ,0)B.(2,0)C.(
,0)B.(2,0)C.(![]() ,0)D.(3,0)
,0)D.(3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .直线
.直线![]() .
.
![]() 抛物线的解析式为 .直线
抛物线的解析式为 .直线![]() 的解析式为 ;
的解析式为 ;
![]() 若直线
若直线![]() 与抛物线只有一个公共点,求直线
与抛物线只有一个公共点,求直线![]() 的解析式;
的解析式;
![]() 设抛物线的顶点关于
设抛物线的顶点关于![]() 轴的对称点为
轴的对称点为![]() ,点
,点![]() 是抛物线对称轴上一动点,如果直线
是抛物线对称轴上一动点,如果直线![]() 与抛物线在
与抛物线在![]() 轴上方的部分形成了封闭图形(记为图形
轴上方的部分形成了封闭图形(记为图形![]() ).请结合函数的图象,直接写出点
).请结合函数的图象,直接写出点![]() 的纵坐标
的纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB中,∠AOB=90°,将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,则![]() 的值为( )
的值为( )
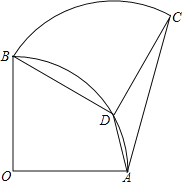
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)形状如图,下列结论:①b>0;②a﹣b+c=0;③当x<﹣1或x>3时,y>0;④一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根.正确的有( )
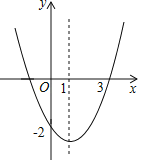
A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com