
【题目】已知抛物线y=ax2+bx+c过点A(0,2)。
(1)若点(-![]() ,0)也在该抛物线上,求a,b满足的关系式;
,0)也在该抛物线上,求a,b满足的关系式;
(2)若点A为抛物线顶点,且抛物线过点(1,1)。
①求抛物线的解析式;
②若点M是抛物线上异于点A的一个动点,点P与点O关于点A对称,直线MP交抛物线与另一个点N,点N’是抛物线上点N关于对称轴的对称点,直线PN’与抛物线交于点E,求证:直线EN恒过点O。
【答案】(1)3a-![]() b=-2;(2)①y=-
b=-2;(2)①y=-![]() +2,②见解析
+2,②见解析
【解析】
(1)由抛物线经过点A可求出c=2,再代入(-![]() ,0)即可找出3a-
,0)即可找出3a-![]() b=-2(a≠0);
b=-2(a≠0);
(2)由A点为抛物线的顶点,可设y=ax2+2,把(1,1)代入求出a的值即可;
(3)设M点的坐标为(m,m2+2)求出直线PM的解析式,与抛物线方程联立,求出N点坐标,根据M点与E点关于y轴对称求出E点坐标,从而求出直线EN的解析式,判断当x=0时,y=0即可.
(1)∵抛物线y=ax2+bx+c过点A(0,2),
∴c=2.
又∵点(-![]() ,0)也在该抛物线上,
,0)也在该抛物线上,
∴a(-![]() )2+b(-
)2+b(-![]() )+c=0,
)+c=0,
∴3a-![]() b+2=0(a≠0).
b+2=0(a≠0).
即3a-![]() b=-2;
b=-2;
(2)∵点A(0,2)是抛物线的顶点坐标,
∴设![]() ,
,
∵函数![]() 的图象经过(1,1)
的图象经过(1,1)
∴1=a+2,解得,a=-1,
∴抛物线的解析式为:![]()
(3)设M点的坐标为(m,-m2+2)(m<0),
设直线PM的解析式为:![]()
∵点P与点O关于点A对称,A(0,2),
∴P(0,4),

∴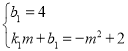 ,
,
解得,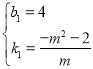 ,
,
∴直线PM的解析式为:![]() ,
,
联立方程组得,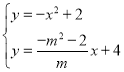
解得, ,
, ,
,
∴N(![]() ,
,![]() ).
).
∵M点与E点关于y轴对称,
∴E(-m,-m2+2)
设直线NE的解析式为:![]() ,
,
将N点、E点坐标代入得,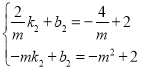 ,解得,
,解得,
∴直线EN的解析式为:![]()
∴当x=0时,y=0,
∴直线EN恒过点O.


科目:初中数学 来源: 题型:
【题目】已知正方形ABCD中,AB=6,点P是射线BC上的一动点,过点P作PE⊥PA交直线CD于E,连AE.

(1)如图1,若BP=2,求DE的长;
(2)如图2,若AP平分∠BAE,连PD,求tan∠DPE的值;
(3)直线PD,AE交于点F,若BC=4PC,则![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() .
.
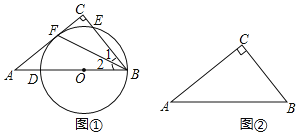
(1)如图①,点![]() 在斜边
在斜边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 长为半径的圆交
长为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,与边
,与边![]() 相切于点
相切于点![]() .求证:
.求证:![]() ;
;
(2)在图②中作![]() ,使它满足以下条件:
,使它满足以下条件:
①圆心在边![]() 上;②经过点
上;②经过点![]() ;③与边
;③与边![]() 相切.
相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.

(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,AC=5,AB=10,
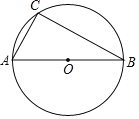
(1)作以AC为底边的圆内接等腰△ACD;(要求:尺规作图,不写作法,保留作图痕迹)
(2)求弦AC所对的圆周角。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,将两个全等的等腰直角三角形![]() 和
和![]() 摆放在一起,
摆放在一起,![]() 为公共顶点,
为公共顶点,![]() ,若
,若![]() 固定不动,
固定不动,![]() 绕点
绕点![]() 旋转,
旋转,![]() 、
、![]() 与边
与边![]() 的交点分别为
的交点分别为![]() 、
、![]() (点
(点![]() 不与点
不与点![]() 重合,点
重合,点![]() 不与点
不与点![]() 重合).
重合).
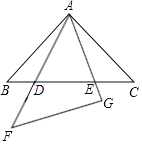
(1)求证:![]() ;
;
(2)在旋转过程中,试判断等式![]() 是否始终成立,若成立,请证明;若不成立,请说明理由.
是否始终成立,若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 为常数,且
为常数,且![]() )中的
)中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
以下结论:
①二次函数![]() 有最小值为
有最小值为![]() ;
;
②当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
③二次函数![]() 的图象与
的图象与![]() 轴只有一个交点;
轴只有一个交点;
④当![]() 时,
时,![]() .
.
其中正确的结论有( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张反面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,将四张纸牌洗匀正面朝下随机放在桌面上.
,其正面分别画有四个不同的几何图形,将四张纸牌洗匀正面朝下随机放在桌面上.
(1)从四张纸牌中随机摸出一张,摸出的牌面图形是中心对称图形的概率是 .
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张,不放回.再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形既是轴对称图形又是中心对称图形,则小亮获胜,否则小明获胜.这个游戏公平吗?请用列表法(或画树状图)说明理由.(纸牌用![]() 表示)若不公平,请你帮忙修改一下游戏规则,使游戏公平.
表示)若不公平,请你帮忙修改一下游戏规则,使游戏公平.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第 24 届冬奥会将于 2022 年在北京和张家口举行,冬奥会的项目有滑雪(如跳台滑雪、高山滑雪、单板滑雪等)、滑冰(如短道速滑、速度滑冰、花样滑冰等)、冰球、冰壶等.如图,有 5 张形状、大小、质地均相同的卡片,正面分别印有高山滑雪、速度滑冰、冰球、单板滑雪、冰壶五种不同的图案,背面完全相同.现将这 5 张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面恰好是滑雪项目图案的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com