
【题目】如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD. 
(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若AB=9,BC=6.求PC的长.
【答案】
(1)解:PC与圆O相切,理由为:
过C点作直径CE,连接EB,如图,
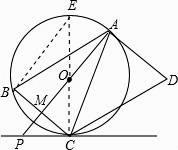
∵CE为直径,
∴∠EBC=90°,即∠E+∠BCE=90°,
∵AB∥DC,
∴∠ACD=∠BAC,
∵∠BAC=∠E,∠BCP=∠ACD.
∴∠E=∠BCP,
∴∠BCP+∠BCE=90°,即∠PCE=90°,
∴CE⊥PC,
∴PC与圆O相切;
(2)解:∵AD是⊙O的切线,切点为A,
∴OA⊥AD,
∵BC∥AD,
∴AM⊥BC,
∴BM=CM= ![]() BC=3,
BC=3,
∴AC=AB=9,
在Rt△AMC中,AM= ![]() =6
=6 ![]() ,
,
设⊙O的半径为r,则OC=r,OM=AM﹣r=6 ![]() ﹣r,
﹣r,
在Rt△OCM中,OM2+CM2=OC2,即32+(6 ![]() ﹣r)2=r2,解得r=
﹣r)2=r2,解得r= ![]() ,
,
∴CE=2r= ![]() ,OM=6
,OM=6 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴BE=2OM= ![]() ,
,
∵∠E=∠MCP,
∴Rt△PCM∽Rt△CEB,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴PC= ![]() .
.
【解析】(1)过C点作直径CE,连接EB,由CE为直径得∠E+∠BCE=90°,由AB∥DC得∠ACD=∠BAC,而∠BAC=∠E,∠BCP=∠ACD,所以∠E=∠BCP,于是∠BCP+∠BCE=90°,然后根据切线的判断得到结论;(2)根据切线的性质得到OA⊥AD,而BC∥AD,则AM⊥BC,根据垂径定理有BM=CM= ![]() BC=3,根据等腰三角形性质有AC=AB=9,在Rt△AMC中根据勾股定理计算出AM=6
BC=3,根据等腰三角形性质有AC=AB=9,在Rt△AMC中根据勾股定理计算出AM=6 ![]() ;设⊙O的半径为r,则OC=r,OM=AM﹣r=6
;设⊙O的半径为r,则OC=r,OM=AM﹣r=6 ![]() ﹣r,在Rt△OCM中,根据勾股定理计算出r=
﹣r,在Rt△OCM中,根据勾股定理计算出r= ![]() ,则CE=2r=
,则CE=2r= ![]() ,OM=6
,OM=6 ![]() ﹣
﹣ ![]() =
= ![]() ,利用中位线性质得BE=2OM=
,利用中位线性质得BE=2OM= ![]() ,然后判断Rt△PCM∽Rt△CEB,根据相似比可计算出PC.
,然后判断Rt△PCM∽Rt△CEB,根据相似比可计算出PC.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上的任意一点 (不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD. 
(1)弦长AB等于(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数;
(3)当AC的长度为多少时,以A、C、D为顶点的三角形与以B、C、0为顶点的三角形相似?请写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD。
(1)图中与∠COE互补的角是___________________; (把符合条件的角都写出来)
(2)如果∠AOC =![]() ∠EOF ,求∠AOC的度数。
∠EOF ,求∠AOC的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B均在函数y= ![]() (k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( )
(k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( ) 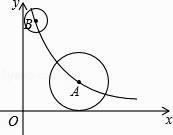
A.(2,2)
B.(2,3)
C.(3,2)
D.(4, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是 .
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,1),直线l:y=﹣1.动点P满足条件:
①P在这个平面直角坐标系中;
②P到A的距离和P到l的距离相等;
(1)求点P所经过的轨迹方程,并在网格中绘制这个图象.(提示:平面直角坐标系中两点之间的距离可以通过勾股定理来求得)
(2)已知直线y=kx+1,小明同学说,这条直线与(1)中所绘的图象有两个交点?你能说明小明为什么这么说吗?
(3)经过了上述的计算、绘图,小明发现,如果第(2)问的两个交点分别为B、C,那么,过BC的中点M作直线l的垂线,垂足为H,连接BH、CH,所得到的三角形BCH是个特殊的三角形,你能说明它是什么三角形吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
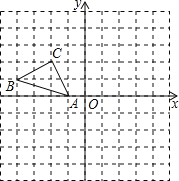
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.
(2)点B1的坐标为 ,点C2的坐标为 .
(3)△ABC经过怎样的旋转可得到△A1B2C2, .
查看答案和解析>>
科目:初中数学 来源: 题型:
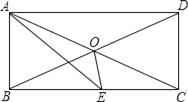
【题目】矩形ABCD中,AC、BD相交于O,AE平分∠BAD交BC于E.
(1)求证:△ABE是等腰直角三角形;
(2)若∠CAE=15°,求证:△ABO是等边三角形;
(3)在(2)的条件下,求∠BOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=BC,将△ABC绕顶点B逆时针方向旋转![]() 度到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
度到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
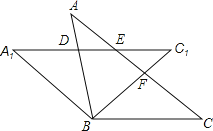
(1)若∠ABC=![]() ,∠DBF=
,∠DBF=![]() ,则
,则![]() =______°;
=______°;
(2)求证:△BCF≌△BA1D;
(3)连接DF,当∠DBF=![]() 时,判定△DBF的形状并说明理由.
时,判定△DBF的形状并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com