
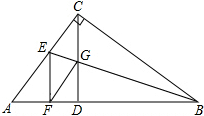
 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BE平分∠ABC交CD、AC分别于G、E,GF∥AC交AB于F.
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BE平分∠ABC交CD、AC分别于G、E,GF∥AC交AB于F.分析 (1)根据垂直的定义得到∠A=∠BCD,由平行线的性质得到∠GFD=∠A,等量代换得到∠BCD=∠GFD,即可得到结论;
(2)根据全等三角形的性质得到BF=BC,证得△CBE≌△BFE,根据全等三角形的性质得到∠EFB=∠ECB=90°,于是得到结论.
解答 证明:(1)∵∠ACB=90°,CD⊥AB,
∴∠A=∠BCD,
∵GF∥AB,
∴∠GFD=∠A,
∴∠BCD=∠GFD,
在△BFG与△BCG中,
$\left\{\begin{array}{l}{∠BCD=∠GFD}\\{∠CBE=∠FBE}\\{BG=BG}\end{array}\right.$,
∴△BFG≌△BCG,
(2)∵△BFG≌△BCG,
∴BF=BC,
在△CBE与△BCG中,
$\left\{\begin{array}{l}{BC=BF}\\{∠CBE=∠FBE}\\{BE=BE}\end{array}\right.$,
∴△CBE≌△BFE,
∴∠EFB=∠ECB=90°,
∴EF⊥AB.
点评 本题考查了直角三角形的性质,平行线的性质,全等三角形的判定与性质,证明三角形全等是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com