
【题目】如图,已知![]() 画射线
画射线![]() ,射线
,射线![]() ,试写出
,试写出![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.

【答案】![]() 或
或![]() ,见解析.
,见解析.
【解析】
分OC、OD在边OA的同侧和异侧分别作出图形,然后分别进行计算即可得解.
∠AOB=∠COD或∠AOB+∠COD=180°,理由如下:
如图1,∵OC⊥OA,OD⊥OB,
∴∠AOB+∠BOC=90°,∠COD+∠BOC=90°,
∴∠AOB=∠COD;
如图2,∵OC⊥OA,OD⊥OB,
∴∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=∠AOB+∠AOD=90°,
∴∠AOB+∠BOC+∠AOB+∠AOD=180°,
又∵∠BOC+∠AOB+∠AOC=∠COD,
∴∠AOB+∠COD=180°;
如图3,∠AOB+∠COD =360°-∠AOC-∠BOD=360°-90°-90°=180°;
如图4,∵OC⊥OA,OD⊥OB,
∴∠AOB+∠AOD=90°,∠COD+∠AOD=90°,
∴∠AOB=∠COD;
综上所述,∠AOB=∠COD或∠AOB+∠COD=180°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是( )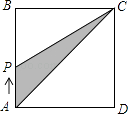
A.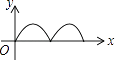
B.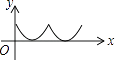
C.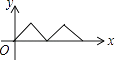
D.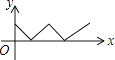
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着智能手机的普及,微信抢红包已成为春节期间人们最喜欢的活动之一,某校七年级(1)班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.
请根据以上信息回答: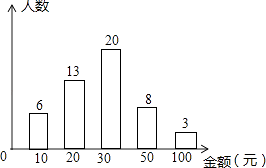
(1)该班同学所抢红包金额的众数是 , 中位数是;
(2)该班同学所抢红包的平均金额是多少元?
(3)若该校共有18个班级,平均每班50人,请你估计该校学生春节期间所抢的红包总金额为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,AC与OB交于点D (8,4),反比例函数y= ![]() 的图象经过点D.若将菱形OABC向左平移n个单位,使点C落在该反比例函数图象上,则n的值为 .
的图象经过点D.若将菱形OABC向左平移n个单位,使点C落在该反比例函数图象上,则n的值为 . 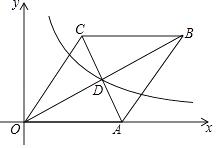
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC∥GE,AF∥DE,点D在直线BC上,点F在直线GE上,且∠1=50°.
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交直线BC于点Q,且∠Q=18°,则∠ACB的度数为______°.(直接写出答案)
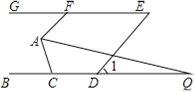
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C是不在同一条直线上的三点,请按下列要求画图并作答(画图时工具不限,不需写出结论,只需画出图形、标注字母):
(1)画直线BC,连接AC;
(2)画线段BC的中点D,连接AD;
(3)画出∠ADC的平分线交AC于点E;
(4)若∠BDA=![]() 求∠ADC,∠EDC.
求∠ADC,∠EDC.

查看答案和解析>>
科目:初中数学 来源: 题型:
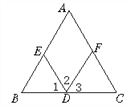
【题目】如图,(1)∵∠A=_____(已知),
∴AC∥ED( )
(2)∵∠2=_____(已知),
∴AC∥ED( )
(3)∵∠A+_____=180°(已知),
∴AB∥FD( )
(4)∵AB∥_____(已知),
∴∠2+∠AED=180°( )
(5)∵AC∥_____(已知),
∴∠C=∠1( )
查看答案和解析>>
科目:初中数学 来源: 题型:
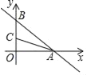
【题目】在平面直角坐标系中,已知一次函数y=﹣![]() x+6与x,y轴分别交于A,B两点,点C(0,n)是线段BO上一点,将△AOB沿直线AC折叠,点B刚好落在x轴负半轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是线段BO上一点,将△AOB沿直线AC折叠,点B刚好落在x轴负半轴上,则点C的坐标是( )
A. (0,3) B. (0,![]() ) C. (0,
) C. (0,![]() ) D. (0,
) D. (0,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com