
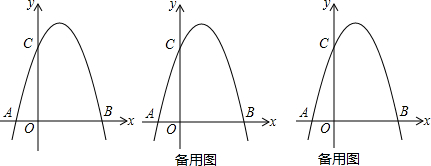
���� ��1�����ݴ���ϵ�������ɵú�������ʽ�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�A��B������ꣻ
��2������ͼ�θ�����ɵö��κ��������ݶ��κ��������ʣ��ɵ���ֵ�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�F�����ꣻ
��3���������ۣ���APΪƽ���ı��εıߣ����ݺ���ֵ��ȵ�������ڶԳ���Գƣ��ɵ�Q�����ꣻ
��APΪƽ���ı��εĶԽ��ߣ�����ƽ���ı��ε����ʣ��ɵù���x�ķ��̣����ݽⷽ�̣��ɵô𰸣�
��� �⣺��1���������ߵĽ���ʽΪy=a��x-1��2+4��
��C��������룬��a+4=3��
���a=-1��
�����ߵĽ���ʽΪy=-��x-1��2+4��
��y=0ʱ��-��x-1��2+4=0��
���x1=-1��x2=3��
��A��������-1��0����B��������3��0����
��2����ͼ1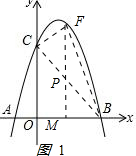 ����FM��x�ύBC��P�㣬
����FM��x�ύBC��P�㣬
BC�Ľ���ʽΪy=-x+3��P��m��-m+3����
F���������ϣ���F��m��-m2+2m+3����
PF=-m2+2m+3-��-m+3��=-m2+3m��
S=S��BCF=S��BPF+SCFP
=$\frac{1}{2}$PF•OM+$\frac{1}{2}$PF•BM
=$\frac{1}{2}$��-m2+3m����3
=-$\frac{3}{2}$m2+$\frac{9}{2}$m��
��m=$\frac{3}{2}$ʱ��S���=$\frac{27}{8}$��
��m=$\frac{3}{2}$ʱ��-m2+2m+3=-$\frac{9}{4}$+3+3=$\frac{15}{4}$��
��F��$\frac{3}{2}$��$\frac{15}{4}$����
��2������ͼ2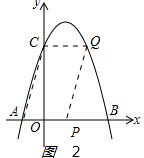 ����AP��ƽ���ı��εı�ʱ��CQ��AP�����Ե�C��Q���������ߵĶԳ���Գƣ���Q1������Ϊ��2��3����
����AP��ƽ���ı��εı�ʱ��CQ��AP�����Ե�C��Q���������ߵĶԳ���Գƣ���Q1������Ϊ��2��3����
����ͼ3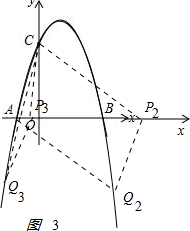 ����AP��ƽ���ı��εĶԽ���ʱ����C��Q�־�x�����࣬C��Q��x��ľ�����ȣ�
����AP��ƽ���ı��εĶԽ���ʱ����C��Q�־�x�����࣬C��Q��x��ľ�����ȣ�
�ⷽ��-x2+2x+3=-3����$x=1��\sqrt{7}$�����Ե�Q2������Ϊ��$1+\sqrt{7}��-3$����Q3 ��$1-\sqrt{7}��-3$����
����������Q1��2��3����Q2��$1+\sqrt{7}��-3$����Q3��$1-\sqrt{7}��-3$����
���� ���⿼���˶��κ����ۺ��⣬���ô���ϵ������������ʽ���Ա����뺯��ֵ�Ķ�Ӧ��ϵ��ͼ����x��Ľ��㣻����ͼ�θ����������������Ĺؼ�������ƽ���ı��ε����ʵó�����Q��ĺ�����ķ����ǽ���ؼ���Ҫ�������ۣ��Է���©��


 �żӾ���ϵ�д�
�żӾ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
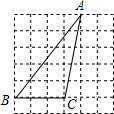 ��ͼ���ڱ߳�Ϊ1��С��������ɵ������У���ABC������������ڸ���ϣ���tan��B��ֵΪ$\frac{5}{4}$��
��ͼ���ڱ߳�Ϊ1��С��������ɵ������У���ABC������������ڸ���ϣ���tan��B��ֵΪ$\frac{5}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��2 | B�� | 3��2 | C�� | 2��-2 | D�� | 3��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com