
分析 根据平方差公式分解因式后计算即可.
解答 解:(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{10{0}^{2}}$)
=$(1-\frac{1}{2})(1+\frac{1}{2})(1-\frac{1}{3})(1+\frac{1}{3})(1-\frac{1}{4})(1+\frac{1}{4})…(1-\frac{1}{100})(1+\frac{1}{100})$
=$\frac{1}{2}×\frac{3}{2}×\frac{2}{3}×\frac{4}{3}×\frac{3}{4}×\frac{5}{4}×…×\frac{99}{100}×\frac{101}{100}$
=$\frac{101}{200}$.
故答案为:$\frac{101}{200}$.
点评 此题考查因式分解的应用,关键是利用平方差公式把原式变形解答.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
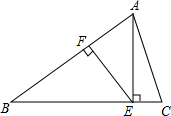 已知:如图,等腰△ABC中,AB=BC,AE⊥BC于E,EF⊥AB于F,若CE=2,cos∠AEF=$\frac{4}{5}$,求BE的长.
已知:如图,等腰△ABC中,AB=BC,AE⊥BC于E,EF⊥AB于F,若CE=2,cos∠AEF=$\frac{4}{5}$,求BE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1)4与-14 | B. | -|-3|与-(-3) | C. | ${\frac{2}{3}^2}与{({\frac{2}{3}})^2}$ | D. | ${({\frac{-1}{3}})^3}与\frac{-1}{3^3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com