
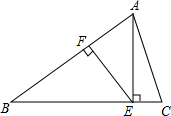
 已知:如图,等腰△ABC中,AB=BC,AE⊥BC于E,EF⊥AB于F,若CE=2,cos∠AEF=$\frac{4}{5}$,求BE的长.
已知:如图,等腰△ABC中,AB=BC,AE⊥BC于E,EF⊥AB于F,若CE=2,cos∠AEF=$\frac{4}{5}$,求BE的长. 分析 根据题意,通过变化可得∠B=∠AEF,CE=2,cos∠AEF=$\frac{4}{5}$,从而可以得到BE、AB的关系,从而可以解答本题.
解答 解:∵AE⊥BC于E,EF⊥AB于F,
∴∠AEB=∠AFE=90°.
∴∠B+∠BAE=∠BAE+∠AEF=90°.
∴∠B=∠AEF.
∵cos∠AEF=$\frac{4}{5}$,
∴cos∠B=$\frac{4}{5}$.
∵cos∠B=$\frac{BE}{AB}$,AB=BC,CE=2,
∴设BE=4a,则AB=5a,CE=a.
∴a=2.
∴BE=8.
点评 本题考查解直角三角形,解题的关键是建立各个角之间的关系,找准所求问题需要的条件.


科目:初中数学 来源: 题型:填空题
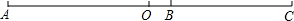 如图:AB=4cm,BC=3cm,如果O是线段AC的中点,求线段OB的长度.(括号内注理由)
如图:AB=4cm,BC=3cm,如果O是线段AC的中点,求线段OB的长度.(括号内注理由)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进出数量 (单位:吨) | -3 | 4 | -1 | 2 | -5 |
| 进出次数 | 2 | 1 | 3 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
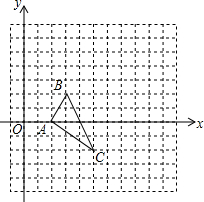 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,0),B(3,2),C(5,-2).以原点O为位似中心,在y轴的右侧将△ABC放大为原来的两倍得到△A′B′C′.
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,0),B(3,2),C(5,-2).以原点O为位似中心,在y轴的右侧将△ABC放大为原来的两倍得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
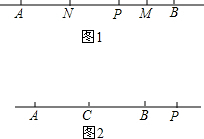 如图1,直线AB上,点P在A、B两点之间,点M为线段PB的中点,点N为线段AP的中点,若AB=m,且m为关于x的方程3x+8=2(x+m)的解.
如图1,直线AB上,点P在A、B两点之间,点M为线段PB的中点,点N为线段AP的中点,若AB=m,且m为关于x的方程3x+8=2(x+m)的解.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com