
分析 (1)观察等式可得an=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),然后根据此规律就可解决问题;
(2)只需运用以上规律,采用拆项相消法即可解决问题.
解答 解:(1)观察等式,可得以下规律:an=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
∴a5=$\frac{1}{9×11}$=$\frac{1}{2}$×($\frac{1}{9}$-$\frac{1}{11}$).
故答案为:$\frac{1}{9×11}$=$\frac{1}{2}$×($\frac{1}{9}$-$\frac{1}{11}$);
(2)a1+a2+a3+…+an=$\frac{1}{2}$×(1-$\frac{1}{3}$)+$\frac{1}{2}$×($\frac{1}{3}$-$\frac{1}{5}$)+$\frac{1}{2}$×($\frac{1}{5}$-$\frac{1}{7}$)+…+$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{49}{99}$,
解得:n=49.
故答案为49.
点评 本题是规律探究题,考查了归纳猜想的能力,运用拆项相消法是解决第(2)小题的关键.


科目:初中数学 来源: 题型:解答题
| 时间(h) | 0 | 5 | 7 | x |
| 甲车位置(km) | 190 | -10 | ||
| 流动加油车位置(km) | 170 | 270 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
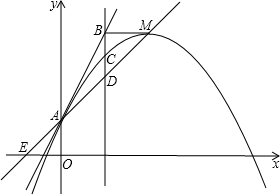 如图,无论非零的a取何值,抛物线y=ax2+bx+c的顶点M都在直线yAE=kx+1上(E、A分别在x轴、y轴上),且OA=OE.
如图,无论非零的a取何值,抛物线y=ax2+bx+c的顶点M都在直线yAE=kx+1上(E、A分别在x轴、y轴上),且OA=OE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
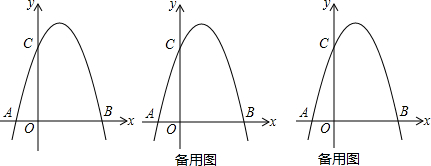
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,BC=8cm,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC.
如图,在△ABC中,BC=8cm,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com