
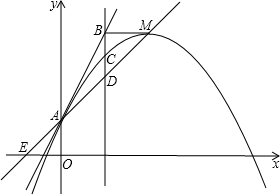
 如图,无论非零的a取何值,抛物线y=ax2+bx+c的顶点M都在直线yAE=kx+1上(E、A分别在x轴、y轴上),且OA=OE.
如图,无论非零的a取何值,抛物线y=ax2+bx+c的顶点M都在直线yAE=kx+1上(E、A分别在x轴、y轴上),且OA=OE.分析 (1)根据直线解析式可得点A的坐标为(0,1),则可得点E的坐标为(-1,0),代入直线解析式,可求出k的值.
(2)将顶点M的坐标代入直线解析式,再由无论a为何值(0除外),其顶点M一定在直线y=kx+1上,可得出b、c的值.
(3)根据抛物线与直线只有一个交点,求出m的值,继而得出B、C、D的坐标,求出BC、CD的长度,即可得出CD和BC的数量关系.
解答 解:(1)∵直线解析式为yAE=kx+1,
∴点A的坐标为(0,1),
又∵OA=OE
∴点E的坐标为(-1,0),
将点E的坐标代入直线解析式可得:0=-k+1,
解得:k=1;
(2)将顶点M的坐标(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)代入y=x+1得:$\frac{4ac-{b}^{2}}{4a}$=-$\frac{b}{2a}$+1.
整理得关于a的一元一次方程:(4c-4)a=b2-2b.
∵该方程有无数个解,
∴4c-4=0,且b2-2b=0.
∴c=1;
又∵b≠0,
∴b=2.
或:取a的两个特殊值1、2,可求得点M的坐标分别为(-$\frac{b}{2}$,$\frac{4c-{b}^{2}}{4}$)、(-$\frac{b}{4}$,$\frac{8c-{b}^{2}}{8}$).
把它们分别代入y=x+1并化简得方程组$\left\{\begin{array}{l}{b^2}-2b=4c-4\\{b^2}-2b=8c-8.\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=2(b≠0)}\\{c=1}\end{array}\right.$.
(3)由(2)知:抛物线的解析式为y=ax2+2x+1.
∴该抛物线经过点A.
由题意知:关于x的一元二次方程ax2+2x+1=mx+1即ax2+(2-m)x=0的△=0.
∴(2-m)2=0.
∴m=2.
∴直线AB的解析式为y=2x+1.
∵yB=yM=1-$\frac{1}{a}$,
把它代入y=2x+1可求得:xB=-$\frac{1}{2a}$.
∵BC⊥x轴分别交抛物线、直线AE于C、D,
∴xC=xD=xB=-$\frac{1}{2a}$.
把它们分别代入y=ax2+2x+1、y=x+1可求得:yC=-$\frac{3}{4a}$+1,yD=-$\frac{1}{2a}$+1.
∴CD=yC-yD=-$\frac{1}{4a}$,BC=yB-yC=-$\frac{1}{4a}$.
∴CD=BC.
点评 本题考查了二次函数的综合题,解题的关键是熟练掌握待定系数法求函数解析式、顶点坐标公式,抛物线与直线的交点问题的知识点,以及方程思想的应用,综合性较强,有一定的难度.


科目:初中数学 来源: 题型:选择题
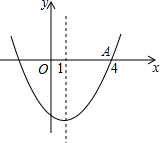 如图,二次函数y=ax2+bx+c图象的对称轴为直线x=1,若其与x轴的一个交点为A(4,0),则由图象可知,该二次函数与x轴的另一个交点坐标是( )
如图,二次函数y=ax2+bx+c图象的对称轴为直线x=1,若其与x轴的一个交点为A(4,0),则由图象可知,该二次函数与x轴的另一个交点坐标是( )| A. | (-4,0) | B. | (-3,0) | C. | (-2,0) | D. | (-1,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0<t<4 | B. | 0≤t<4 | C. | 0<t<1 | D. | t≥0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
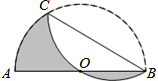 如图,AB是半圆O的直径,且AB=12,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是6π.(结果保留π)
如图,AB是半圆O的直径,且AB=12,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是6π.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
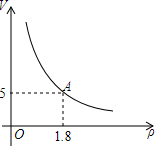 如图,一定质量的氧气,其体积V(m3)是密度ρ(kg/m3)的反比例函数,其图象如图,求:
如图,一定质量的氧气,其体积V(m3)是密度ρ(kg/m3)的反比例函数,其图象如图,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一张桌子上摆放有若干个形状、大小完全相同的碟子,现从三个方向看,看到的图形如图所示,则这张桌子上碟子的总数可能是( )
一张桌子上摆放有若干个形状、大小完全相同的碟子,现从三个方向看,看到的图形如图所示,则这张桌子上碟子的总数可能是( )| A. | 11 | B. | 14 | C. | 18 | D. | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com