
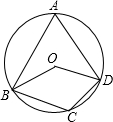
 已知:如图,四边形ABCD内接于⊙O,∠BOD=120°,∠BAD=60°,∠BCD=120°.
已知:如图,四边形ABCD内接于⊙O,∠BOD=120°,∠BAD=60°,∠BCD=120°.  黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:选择题
| A. | 两个负数,绝对值大的大 | |
| B. | 在数轴上表示两个负数,离原点远的那个数小 | |
| C. | 两个数比较大小,绝对值大的反而小 | |
| D. | 在数轴上,两个负数中大的离原点远 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.完成以下解答过程中的空缺部分:
如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.完成以下解答过程中的空缺部分:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
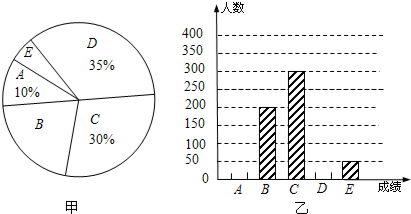
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
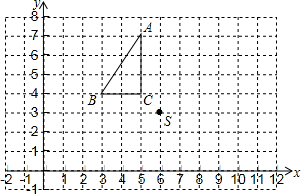 △ABC和点S在平面直角坐标系中的位置如图所示.
△ABC和点S在平面直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一次函数的表达式为y=2x+4.
已知一次函数的表达式为y=2x+4.| x | … | -2 | -1 | 0 | 1 | 2 | … |
| Y | … | 8 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com