
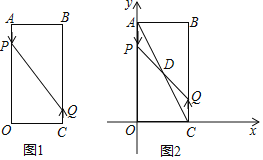
【题目】如图1,已知矩形AOCB,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动.
(1)点P到达终点O的运动时间是 s,此时点Q的运动距离是 cm;
(2)当运动时间为2s时,P、Q两点的距离为 cm;
(3)请你计算出发多久时,点P和点Q之间的距离是10cm;
(4)如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连结AC,与PQ相交于点D,若双曲线y=![]() 过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.
过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)t=
;(3)t=![]() 或t=
或t=![]() ;(4)
;(4)![]() .
.
【解析】
(1)先求出OA,进而求出时间,即可得出结论;
(2)构造出直角三角形,再求出PE,QE,利用勾股定理即可得出结论;
(3)同(2)的方法利用勾股定理建立方程求解即可得出结论;
(4)先求出直线AC解析式,再求出点P,Q坐标,进而求出直线PQ解析式,联立两解析式即可得出结论.
(1)∵四边形AOCB是矩形,
∴OA=BC=16,
∵动点P从点A出发,以3cm/s的速度向点O运动,
∴t=![]() ,此时,点Q的运动距离是
,此时,点Q的运动距离是![]() ×2=
×2=![]() cm;
cm;
(2)如图1,由运动知,AP=3×2=6cm,CQ=2×2=4cm,
过点P作PE⊥BC于E,过点Q作QF⊥OA于F,
∴四边形APEB是矩形,
∴PE=AB=6,BE=6,
∴EQ=BC﹣BE﹣CQ=16﹣6﹣4=6,
根据勾股定理得,PQ=6![]() ;
;
(3)设运动时间为t秒时,
由运动知,AP=3t,CQ=2t,
同(2)的方法得,PE=6,EQ=16﹣3t﹣2t=16﹣5t,
∵点P和点Q之间的距离是10cm,
∴62+(16﹣5t)2=100,
∴t=![]() 或t=
或t=![]() ;
;
(4)k的值是不会变化,
理由:∵四边形AOCB是矩形,
∴OC=AB=6,OA=16,
∴C(6,0),A(0,16),
∴直线AC的解析式为y=﹣![]() x+16①,
x+16①,
设运动时间为t,
∴AP=3t,CQ=2t,
∴OP=16﹣3t,
∴P(0,16﹣3t),Q(6,2t),
∴PQ解析式为y=![]() x+16﹣3t②,
x+16﹣3t②,
联立①②解得,x=![]() ,y=
,y=![]() ,
,
∴D(![]() ,
,![]() ),
),
∴k=![]() ×
×![]() =
=![]() 是定值.
是定值.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
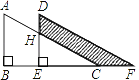
【题目】如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分面积是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:直线及直线外一点![]() .
.

求作:![]() ,使得
,使得![]() .
.
作法:如图,
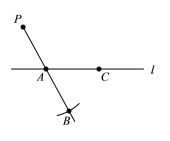
①在直线上取一点![]() ,作射线
,作射线![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 的延长线于点
的延长线于点![]() ;
;
②在直线上取一点![]() (不与点
(不与点![]() 重合),作射线
重合),作射线![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 的延长线于点
的延长线于点![]() ;
;
③作直线![]() .
.
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵![]() _______,
_______,![]() _______,
_______,
∴![]() (____________)(填推理的依据).
(____________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,动点P按图中箭头所示方向从原点出发,第1次运动到P1(1,1),第2次接着运动到点P2(2,0),第3次接着运动到点P3(3,-2),…,按这的运动规律,点P2019的坐标是_____.
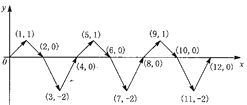
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)直接写出点C的坐标.
(2)在y轴上是否存在点P,使得S△POB=![]() S△ABC若存在,求出点P的坐标;若不存在,请说明理由.
S△ABC若存在,求出点P的坐标;若不存在,请说明理由.
(3)把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探究∠HBM,∠BMA,∠MAC之间的数量关系,并证明你的结论.
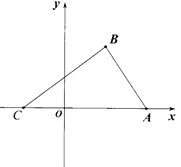
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生上学的交通方式,现从全校学生中随机抽取了部分学生进行“我上学的交通方式”问卷调查,规定每人必须并且只能在“乘车”、“步行”、“骑车”和“其他”四项中选择一项,并将统计结果绘制了如下两幅不完整的统计图.
请解答下列问题:
(1)在这次调查中,该学校一共抽样调查了 名学生;
(2)补全条形统计图;
(3)若该学校共有1500名学生,试估计该学校学生中选择“步行”方式的人数.
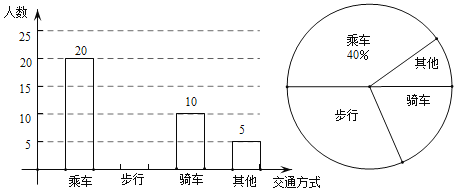
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC,如图,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF.
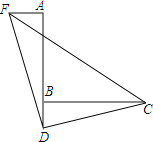
(1)求证:△FAD≌△DBC;
(2)判断△CDF的形状并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
科目:初中数学 来源: 题型:
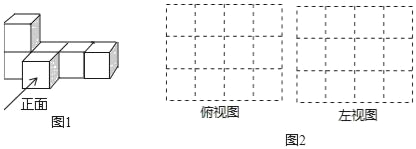
【题目】(1)如图1是由大小相同的小立方块搭成的几何体,请在图2的方格中画出从上面和左面看到的该几何体的形状图.(只需用2B铅笔将虚线化为实线)
(2)若要用大小相同的小立方块搭一个几何体,使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同,则搭这样的一个几何体最多需要 个小立方块.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com