
【题目】如图,在四边形![]() 中,
中,![]() 、
、![]() 为对角线,点
为对角线,点![]() 、
、![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 、
、![]() 边的中点,下列说法:
边的中点,下列说法:
①当![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.②当
四点共圆.②当![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.③当
四点共圆.③当![]() 且
且![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.其中正确的是( )
四点共圆.其中正确的是( )

A. ①② B. ①③ C. ②③ D. ①②③
【答案】C
【解析】
连接EM,MF,FN,NE,连接EF,MN,交于O,利用三角形中位线定理可证明四边形ENFM为平行四边形,然后根据判定出ENFM的形状,可知M,E,N,F是否共圆.
连接EM,ME,FN,NE,FE,NM,交于点O,
∵M,E,N,F为AD,AB,CB,CD的中点,
∴EM∥BD∥NF,EN∥AC∥ME,EM=NF=![]() BD,EN=MF=
BD,EN=MF=![]() AC,
AC,
∴四边形ENFM为平行四边形.
当AC=BD,则有EM=EN,所以平行四边形ENFM是菱形,而菱形的四个顶点不一定共圆,故①不一定成立,
当AC⊥BD时,由EMBD,EN∥AC,EM∥EN,可得:∠MEN=90°,所以平行四边形ENFM为矩形,则有OE=ON=OF=OM,所以E,M,N,F四点共圆,正确
当AC=BD且AC⊥BD,同理可得四边形ENFM为正方向,则有OE=ON=OF=OM,所以MENF四点共圆,正确,
所以答案选择C项.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() 是对角线,
是对角线,![]() ,
,![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.


(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .设
.设![]() ,点
,点![]() 是直线
是直线![]() 上的动点,当
上的动点,当![]() 的值最小时,点
的值最小时,点![]() 与点
与点![]() 是否可能重合?若可能,请说明理由并求此时
是否可能重合?若可能,请说明理由并求此时![]() 的值(用含
的值(用含![]() 的式子表示);若不可能,请说明理由.
的式子表示);若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a使关于x的不等式组 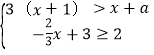 有两个整数解,且使关于x的方程
有两个整数解,且使关于x的方程![]() 有负数解,则符合题意的整数a的个数有 ( )
有负数解,则符合题意的整数a的个数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OA=12cm,OB=8cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,并且它们的运动时间也相等.
(1)请用直尺和圆规作出C处的位置,不必叙述作图过程,保留作图痕迹;
(2)求线段OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的直角坐标系中,解答下列问题.
(1)分别写出A、B两点的坐标:A ,B .
(2)△ABC的面积= ;点B到AC的距离= .
(3)画出△ABC关于x轴对称的△A1B1C1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题(不写作法)已知:如图,在平面直角坐标系中.
(1)作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1三个顶点的坐标;
(2)求△ABC的面积;
(3)在x轴上画点P,使PA+PC最小.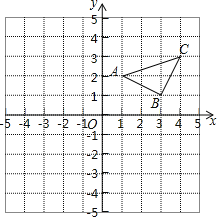
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 和
和![]() 是两个边长都为
是两个边长都为![]() 的等边三角形,且点
的等边三角形,且点![]() ,
,![]() ,
,![]() ,
,![]() 在同一直线上,连接
在同一直线上,连接![]() ,
,![]() .
.
![]() 求证:四边形
求证:四边形![]() 是平行四边形;
是平行四边形;
![]() 若
若![]() 沿着
沿着![]() 的方向匀速运动,
的方向匀速运动,![]() 不动,当
不动,当![]() 运动到点
运动到点![]() 与点
与点![]() 重合时,四边形
重合时,四边形![]() 是什么特殊的四边形?说明理由.
是什么特殊的四边形?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示.
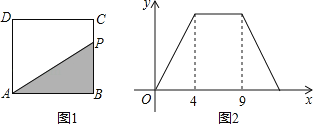
(1)求△ABC的面积;
(2)求y关于x的函数解析式;
(3)当△ABP的面积为5时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】拉杆箱是人们出行的常用品,采用拉杆箱可以让人们出行更轻松.如图,一直某种拉杆箱箱体长AB=65cm,拉杆最大伸长距离BC=35cm,在箱体底端装有一圆形滚轮,当拉杆拉到最长时,滚轮的圆心在图中的A处,点A到地面的距离AD=3cm,当拉杆全部缩进箱体时,滚轮圆心水平向右平移55cm到A′处,求拉杆把手C离地面的距离(假设C点的位置保持不变).
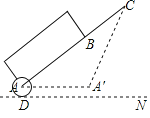
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com