
分析 通过观察可以发现等号左边有连续的自然数“1,2,3,4,…”,“5,6,7,8,…”和定值4,易得每个式子中“×”前后的两个数字相差4,从而得到一般式:n(n+4)+4,根据完全平方公式可知n(n+4)+4=n2+4n+4=(n+2)2;把等号右边对应的数字代入关系式即可验证此等式成立,进一步可求出522=(50+2)2=50×(50+4)+4=50×54+4.
解答 解:观察算式:1×5+4=32
2×6+4=42,
3×7+4=52,
4×8+4=62,可发现:
等号左边:“×”前面的数字是连续的自然数1,2,3,4,…,n;“×”后面的数字也是连续的自然数5,6,7,8,…(n+4);“+”后面的数字是定值4;
等号右边:32=(1+2)2,42=(2+2)2,52=(3+2)2,62=(4+2)2,…(n+2)2;
所以这组算式的一般规律为:n(n+4)+4=(n+2)2;
因为522=(50+2)2=50×(50+4)+4=50×54+4
所以50×54+4=522.
故答案为:50,54,4.
点评 解本题的关键是找到等号两边变化的数字之间的连续性,再结合完全平方公式得出一般规律后,再去求解.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
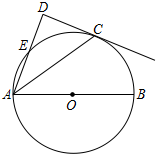 如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AD交⊙O于点E
如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AD交⊙O于点E查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为8”出现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
| “和为8”出现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果2x=2y+1,那么x=y+1 | B. | 如果2=5+3x,那么3x=5-2 | ||
| C. | 如果x-3=y-3,那么x=y | D. | 如果-8x=4,那么x=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
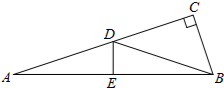 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与AC,AB的交点分别为D,E.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与AC,AB的交点分别为D,E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com