Question

19．如图，直角坐标系中，已知点A（-4，0），B（0，3），将△AOB连续作旋转变换，依次得到三角形①，②，③，④，…，则第19个三角形中顶点A的坐标是（72，4）．

Answer 1

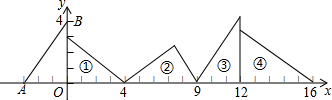
分析 先利用勾股定理计算出AB=5，再观察图中△AOB旋转变换得到△AOB连续作三次旋转变换回到原来的状态，每一个循环三角形向右移动了12个单位，而19=3×6+1，于是可判断第19个三角形的状态与第1个一样，然后写出A点坐标．

解答 解：∵A（-4，0），B（0，3），
∴OA=4，OB=3，
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∵△AOB连续作三次旋转变换回到原来的状态，
而19=3×6+1，
∴第19个三角形的状态与第1个一样，
∴第19个三角形中顶点A的横坐标为6×12=72，纵坐标是4，
即第19个三角形中顶点A的坐标是（72，4）．
故答案为（72，4）．

点评 本题考查了坐标与图形变化-旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．解决本题的关键是找出三角形各顶点坐标的变化规律．