
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3+2$\sqrt{2}$=5$\sqrt{2}$ | C. | 2$\sqrt{3}$×3$\sqrt{3}$=18 | D. | $\sqrt{2}$÷$\sqrt{3}$=$\frac{\sqrt{6}}{2}$ |
分析 根据二次根式的加减法对A、B进行判断;根据二次根式的乘法法则对C进行判断;根据二次根式的除法法则对D进行判断.
解答 解:A、$\sqrt{2}$与$\sqrt{3}$不能合并,所以A选项错误;
B、3与2$\sqrt{2}$不能合并,所以B选项错误;
C、原式=6×3=18,所以C选项正确;
D、原式=$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{2}×\sqrt{3}}{\sqrt{3}×\sqrt{3}}$=$\frac{\sqrt{6}}{3}$,所以D选项错误.
故选C.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:选择题
| A. | 4.3×106米 | B. | 4.3×10-5米 | C. | 4.3×10-6米 | D. | 43×107米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
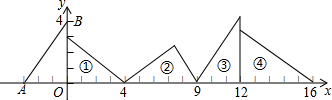
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{m+n}{2}$ | B. | $\frac{m-n}{2}$ | C. | $\frac{m+n}{2}或\frac{m-n}{2}$ | D. | $\frac{1}{2}mn$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+1=0 | B. | x2+4x-4=0 | C. | x2+x+$\frac{1}{4}$=0 | D. | x2-x+$\frac{1}{2}$=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com