Question

3．已知点P到⊙O最远点的距离是m，最近点的距离为n，则这个圆的半径是（　　）

• A． $\frac{m+n}{2}$
• B． $\frac{m-n}{2}$
• C． $\frac{m+n}{2}或\frac{m-n}{2}$
• D． $\frac{1}{2}mn$

Answer 1

分析 已知的点可能在圆外，也可能在圆内，分两种情况进行讨论．

解答 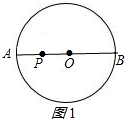解：本题没有明确告知点的位置，应分点在圆内与圆外两种情况，
①当点P在⊙O内时，如图1所示：
此时PA=n，PB=m，
∴AB=m+n，
因此半径为$\frac{m+n}{2}$；
②当点P在⊙O外时，如图2所示：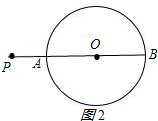
此时PA=n，PB=m，直线PB过圆心O，
直径AB=PB-PA=m-n，
因此半径为$\frac{m-n}{2}$；
综上所述：这个圆的半径为$\frac{m+n}{2}$或$\frac{m-n}{2}$；
故选：C．

点评 本题考查了点与圆的位置关系；解决本题要注意点与圆的位置关系，这个点可能在圆外也可能在圆内，所以分两种情况讨论是解决问题的关键．