
����Ŀ����ѧ�о����֣���ƽ�����ѹԼ��100ǧ�������溣�����߶����ͣ�����3000�����£�ÿ����100�ף���ѹ�½�Լ1ǧ����3000��5000��ÿ����100�ף���ѹ�½�Լ0.8ǧ����ɽ�ĺ��θ߶�Ϊx�ף���Ӧ�Ĵ���ѹΪyǧ����
��1����0��x��3000ʱ����y��x֮��ĺ�����ϵʽ��
��2����ĩ��С����С����ɽ��ɽ�庣��С��5000�ף����棬��ɽ����ô���ѹΪ63.6ǧ�������ɽ�庣��ԼΪ�����ף�
���𰸡���1����0��x��3000ʱ�� y����0.01x+100����2����ɽ�庣��ԼΪ3800�ף�
��������
��1����ÿ����100�ף���ѹ�½�Լ1ǧ���г�������ϵʽ����2����x=3000�������ʽ��ֵ��ȷ��63.6ǧ����Ӧ�ĺ��θ߶���3000�����ϣ��Ӷ���������θ߶�.
�⣺��1��������ɵã�
��0��x��3000ʱ��y��x֮��ĺ�����ϵʽ�ǣ�y��100��![]() ��1����0.01x+100��
��1����0.01x+100��
����0��x��3000ʱ��y��x֮��ĺ�����ϵʽ��y����0.01x+100��
��2����x��3000ʱ��y����0.01��3000+100��70��
��63.6��70��
���ɽ�庣��ԼΪ��![]() ��100+3000��3800���ף���
��100+3000��3800���ף���
����ɽ�庣��ԼΪ3800�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ��ֱ������ϵ�У�����y=ax+b��y=ax2��bx��ͼ������ǣ� ��
A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
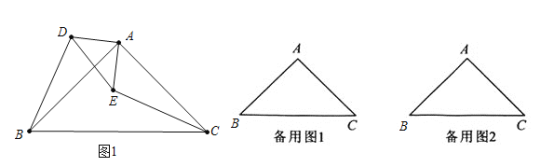
����Ŀ����ͼ��![]() ��
��![]() ���ǵ���ֱ�������Σ�
���ǵ���ֱ�������Σ�![]() ����PΪ����BD��CE�Ľ��㣮
����PΪ����BD��CE�Ľ��㣮
![]() ��֤��
��֤��![]() ��
��
![]() ��
��![]() ����
����![]() �Ƶ�A��ת��
�Ƶ�A��ת��
![]() ��
��![]() ʱ����PB�ij���
ʱ����PB�ij���
![]() ֱ��д����ת�������߶�PB�������ֵ����Сֵ��
ֱ��д����ת�������߶�PB�������ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�꼶��֯ѧ���μ�����Ӫ�����������Ӫ��Ϊ�ס��ҡ���������л����������ͳ��ͼ��ӳ��ѧ�������μ�����Ӫ��������������ͼ�е���Ϣ�ش��������⣺
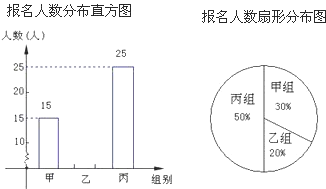
��1�����꼶�����μӱ��������Ϊ ��
��2�����꼶�����μӱ��λ�������� ������ȫƵ���ֲ�ֱ��ͼ��
��3������ʵ���������Ӽ���������ͬѧ�����飬ʹ���������Ǽ���������3����Ӧ�Ӽ�����������ѧ�������飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������x����������㼰�䶥�㹹�ɵȱ������Σ���Ƹ������ߡ��ȱ������ߡ�.
(1)��������m��n����M(m��n)�͵�N��-m+4��n�����ڡ��ȱ������ߡ�![]() ��
��![]() �ϣ���������
�ϣ���������![]() �Ľ���ʽ��
�Ľ���ʽ��
(2)��������![]() ��
��![]() ���ȱ������ߡ�����
���ȱ������ߡ�����![]() ��ֵ��
��ֵ��
(3)���ڡ��ȱ������ߡ�![]() ��
��![]() ����1<x<m�����ܴ���ʵ��b��ʹ���κ���
����1<x<m�����ܴ���ʵ��b��ʹ���κ���![]() ��ͼ����һ�κ���y=xͼ����·�����m�����ֵ.
��ͼ����һ�κ���y=xͼ����·�����m�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=ax2+bx+c��a��0����ͼ����ͼ������5�����ۣ�������ȷ�Ľ����У�������
��abc��0
��3a+c��0
��4a+2b+c��0
��2a+b=0
��b2��4ac
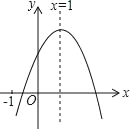
A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2+bx+c(a��0)�IJ���ͼ����ͼ��ʾ��ͼ�����(��1��0)���Գ���Ϊֱ��x��2�����н��ۣ�(1)4a+b��0(2)9a��3bc��(3)9a+b+c��0��(4)������a(x+1)(x��5)����2������Ϊx1��x2����x1��x2����x1��1��5��x2��������ȷ�Ľ�����( )
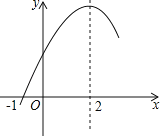
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵxOy�У���ABΪб�ߵĵ���ֱ��������ABC�����е�A��0��2������C����1��0����������y��ax2+ax��2����B�㣮
��1����B������ꣻ
��2���������ߵĽ���ʽ��
��3�������������Ƿ���ڵ�N����B���⣩��ʹ�á�ACN��Ȼ����ACΪֱ�DZߵĵ���ֱ�������Σ������ڣ����N�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У���P��AD�ϣ�AB=2��AP=1.ֱ�dzߵ�ֱ�Ƕ�����ڵ�P����ֱ�dzߵ����߷ֱ�AB��BC�ڵ�E��F������EF(��ͼ1).
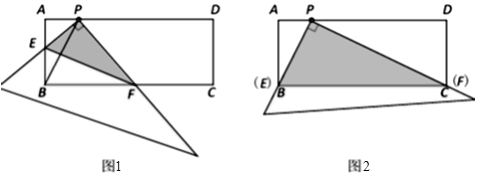
(1)����E���B�غ�ʱ����Fǡ�����C�غ�(��ͼ2).
����֤����APB�ס�DCP��
����PC��BC�ij�.
(2)̽������ֱ�dzߴ�ͼ2�е�λ�ÿ�ʼ���Ƶ�P˳ʱ����ת������E�͵�A�غ�ʱֹͣ.�����������(ͼ1�Ǹù��̵�ij��ʱ��)���۲졢���벢���
�� tan��PEF��ֵ�Ƿ����仯����˵������.
�� ��AE=x������PBF�ǵ���������ʱ����ֱ��д��x��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com