
【题目】汽车租赁行业现在火爆起来.小明开办了一家汽车租赁公司,拥有汽车20辆,在旺季每辆车的每天租金为600元时,可全部租出:当每辆车的每天租金增加50元时,未租出的车将增加一辆,租出的车辆每辆每天需要维护费200元,未租出的车辆每辆每天需要维护费100元,每天其他开销共计1000元.
(1)当每辆车的租金为1000元时,每天能租出多少辆车?每天净收益为多少元?
(2)当每辆车的每天租金定为多少元时,租赁公司的每天净收益最大?最大净收益为多少元?(每天净收益=总租金﹣租出去车辆维护费﹣未租出去车辆维护费﹣每天其他开销)
【答案】(1)当每辆车的租金为1000元时,每天能租出12辆车,每天净收益为7800元;(2)当每辆车的每天租金定为850元时,租赁公司的每天净收益最大,最大净收益为8250元.
【解析】
(1)根据:租出的车=20﹣![]() , 每天净收益=总租金﹣租出去车辆维护费﹣未租出去车辆维护费﹣每天其他开销,列式计算可得;
, 每天净收益=总租金﹣租出去车辆维护费﹣未租出去车辆维护费﹣每天其他开销,列式计算可得;
(2)根据:每天净收益=总租金﹣租出去车辆维护费﹣未租出去车辆维护费﹣每天其他开销列出函数关系式,根据二次函数性质可得最值情况.
(1)当每辆车的租金为x元时,每天租出的车有:20﹣ ![]() =12(辆),每天的净收益为:12×(1000﹣200)﹣8×100﹣1000=7800元,答:当每辆车的租金为1000元时,每天能租出12辆车,每天净收益为7800元.
=12(辆),每天的净收益为:12×(1000﹣200)﹣8×100﹣1000=7800元,答:当每辆车的租金为1000元时,每天能租出12辆车,每天净收益为7800元.
(2)设每辆车每天的租金为x元,每天的净收益为y元,根据题意,得:y=(x﹣200)(20﹣ ![]() )﹣
)﹣![]() ×100﹣1000
×100﹣1000
=﹣![]() x2+34x﹣6200.
x2+34x﹣6200.
∵a=﹣![]() <0,∴当x=﹣
<0,∴当x=﹣ ![]() =850元时,y取得最大值8250元,答:当每辆车的每天租金定为850元时,租赁公司的每天净收益最大,最大净收益为8250元.
=850元时,y取得最大值8250元,答:当每辆车的每天租金定为850元时,租赁公司的每天净收益最大,最大净收益为8250元.


科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
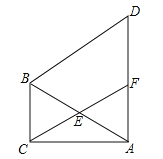
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)若AB=6,求平行四边形BCFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
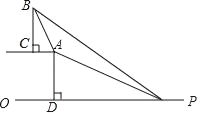
【题目】已知,如图,在坡顶A处的同一水平面上有一座大型纪念碑BC,某同学在斜坡底P处测得该碑的碑顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米到达坡顶A,在坡顶A处又测得该碑的碑顶B的仰角为76°,求纪念碑BC的高度(结果精确到0.1米).(过点A作AD⊥PO,垂足为点D.坡度=AD:PD)(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
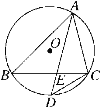
【题目】如图,在△ABC中,∠BAC的平分线AD交BC于E,交△ABC的外接圆⊙O于D.
(1)求证:△ABE∽△ADC;
(2)连接BD,OB,OC,OD,且OD交BC于点F,若点F恰好是OD的中点.求证:四边形OBDC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,然后解答提出的问题:
设 m,n 是有理数,且满足 m+![]() n=2﹣3
n=2﹣3 ![]() ,求 nm 的值.
,求 nm 的值.
解:由题意,移项得,(m﹣2)+(n+3)![]() =0,
=0,
∵m、n 是有理数,∴m﹣2,n+3 也是有理数,
又∵ ![]() 是有理数,∴m﹣2=0,n+3=0,∴m=2,n=﹣3
是有理数,∴m﹣2=0,n+3=0,∴m=2,n=﹣3
∴nm=(﹣3)2=9.
问题解决:设 a、b 都是有理数,且 a2+b![]() =16+5
=16+5![]() ,求2
,求2![]() ﹣5b的值.
﹣5b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com