
【题目】已知,如图,在坡顶A处的同一水平面上有一座大型纪念碑BC,某同学在斜坡底P处测得该碑的碑顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米到达坡顶A,在坡顶A处又测得该碑的碑顶B的仰角为76°,求纪念碑BC的高度(结果精确到0.1米).(过点A作AD⊥PO,垂足为点D.坡度=AD:PD)(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
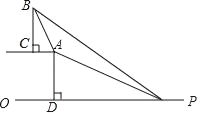
【答案】古塔BC的高度约为18.7米.
【解析】
延长BC交OP于H.在Rt△APD中解直角三角形求出AD=10.PD=24.由题意BH=PH.设BC=x.则x+10=24+DH.推出AC=DH=x﹣14.在Rt△ABC中.根据tan76°=![]() ,构建方程求出x即可.
,构建方程求出x即可.
延长BC交OP于H.
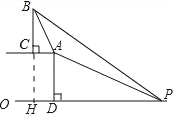
∵斜坡AP的坡度为1:2.4,
∴![]() ,
,
设AD=5k,则PD=12k,由勾股定理,得AP=13k,
∴13k=26,
解得k=2,
∴AD=10,
∵BC⊥AC,AC∥PO,
∴BH⊥PO,
∴四边形ADHC是矩形,CH=AD=10,AC=DH,
∵∠BPD=45°,
∴PH=BH,
设BC=x,则x+10=24+DH,
∴AC=DH=x﹣14,
在Rt△ABC中,tan76°=![]() ,即
,即![]() ≈4.01.
≈4.01.
解得:x≈18.7,
经检验x≈18.7是原方程的解.
答:古塔BC的高度约为18.7米.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源: 题型:
【题目】问题探究
(1)如图1,已知锐角△ABC中,点D在BC边上,当线段AD最短时,请你在图中画出点D的位置.
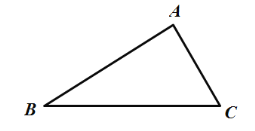
图1
(2)若一个四边形的四个顶点分别在一个三角形的三条边上;则称这个四边形为该三角形的内接四边形.
如图2,在Rt△ABC中,AB=6,BC=8,∠B=90°.矩形BEFG是△ABC的内接矩形,若EF=2,则矩形BEFG的面积为_________
如图3,在△ABC中,AB=![]() ,BC=8,∠B=45°,矩形DEFG是△ABC的一个内接矩形且D、E在边BC上.若EF=2,求矩形DEFG的面积;
,BC=8,∠B=45°,矩形DEFG是△ABC的一个内接矩形且D、E在边BC上.若EF=2,求矩形DEFG的面积;
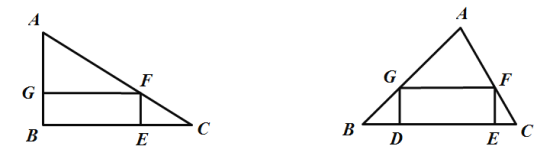
图2 图3
问题解决:
(3)如图4,△ABC是一块三角形木板余料,AB=6,BC=8,∠B=30°,木匠师傅想利用它裁下一块矩形DEFG木块,矩形DEFG是△ABC的一个内接矩形且D、E在边BC上,请在图4中画出对角线DF最短的矩形DEFG,请说明理由,并求出此时DF的长度.
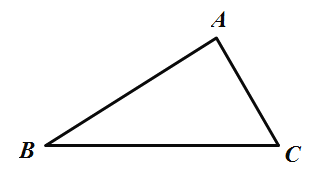
图4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:ABCD是菱形;
(2)若AB=5,AC=6,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A在y轴上,且点A坐标为(0,4),BC在x轴正半轴上,点C在B点右侧,反比例函数![]() (x>0)的图象分别交边AD,CD于E,F,连结BF,已知,BC=k,AE=
(x>0)的图象分别交边AD,CD于E,F,连结BF,已知,BC=k,AE=![]() CF,且S四边形ABFD=20,则k= _________.
CF,且S四边形ABFD=20,则k= _________.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/1/17/2120855162306560/2123559773659136/STEM/85e8312ee4314e6b84d61ad733d78d14.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车租赁行业现在火爆起来.小明开办了一家汽车租赁公司,拥有汽车20辆,在旺季每辆车的每天租金为600元时,可全部租出:当每辆车的每天租金增加50元时,未租出的车将增加一辆,租出的车辆每辆每天需要维护费200元,未租出的车辆每辆每天需要维护费100元,每天其他开销共计1000元.
(1)当每辆车的租金为1000元时,每天能租出多少辆车?每天净收益为多少元?
(2)当每辆车的每天租金定为多少元时,租赁公司的每天净收益最大?最大净收益为多少元?(每天净收益=总租金﹣租出去车辆维护费﹣未租出去车辆维护费﹣每天其他开销)
查看答案和解析>>
科目:初中数学 来源: 题型:
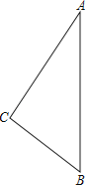
【题目】一名徒步爱好者来衡阳旅行,他从宾馆C出发,沿北偏东30°的方向行走2000米到达石鼓书院A处,参观后又从A处沿正南方向行走一段距离,到达位于宾馆南偏东45°方向的雁峰公园B处,如图所示.
(1)求这名徒步爱好者从石鼓书院走到雁峰公园的途中与宾馆之间的最短距离;
(2)若这名徒步爱好者以100米/分的速度从雁峰公园返回宾馆,那么他在15分钟内能否到达宾馆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程x2-2(m+1)x+m2=0.
(1)当m取何值时,方程有两个实数根?
(2)为m选取一个合适的整数,使方程有两个不相等的实数根,并求这两个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
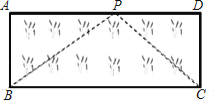
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com