
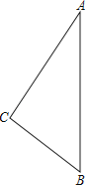
【题目】一名徒步爱好者来衡阳旅行,他从宾馆C出发,沿北偏东30°的方向行走2000米到达石鼓书院A处,参观后又从A处沿正南方向行走一段距离,到达位于宾馆南偏东45°方向的雁峰公园B处,如图所示.
(1)求这名徒步爱好者从石鼓书院走到雁峰公园的途中与宾馆之间的最短距离;
(2)若这名徒步爱好者以100米/分的速度从雁峰公园返回宾馆,那么他在15分钟内能否到达宾馆?
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
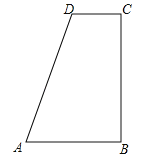
【题目】如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD.
(1)利用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法);
(2)在(1)的条件下,①证明:AE⊥DE;
②若CD=2,AB=4,点M,N分别是AE,AB上的动点,求BM+MN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90,AC=4cm,BC=3cm,点P由点B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由点A出发沿AC方向向点C匀速运动,速度为2cm/s;连结PQ。若设运动时间为t(s)(0<t<2),解答下列问题:

(1)当t为何值时?PQ//BC?
(2)设△APQ的面积为y(cm2),求y与t之间的函数关系?
(3)是否存在某一时刻t,使线段PQ恰好把△ABC的周长和面积同时平分?若存在求出此时t的值;若不存在,说明理由。
(4)如图2,连结PC,并把△PQC沿AC翻折,得到四边形PQP'C,那么是否存在某一时刻t,使四边形PQP'C为菱形?若存在求出此时t的值;若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
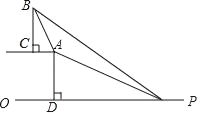
【题目】已知,如图,在坡顶A处的同一水平面上有一座大型纪念碑BC,某同学在斜坡底P处测得该碑的碑顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米到达坡顶A,在坡顶A处又测得该碑的碑顶B的仰角为76°,求纪念碑BC的高度(结果精确到0.1米).(过点A作AD⊥PO,垂足为点D.坡度=AD:PD)(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=ax2+bx+c(a≠0)的图象如图,有下列 5 个结论:①4a+2b+c>0;②abc<0;③b<a+c;④3b>2c;⑤a+b<m(am+b),(m≠1 的实数);其中正确结论的个数为( )
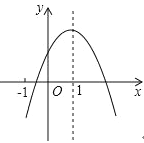
A. 2 个 B. 3 个 C. 4 个 D. 5 个
查看答案和解析>>
科目:初中数学 来源: 题型:
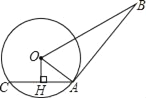
【题目】如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过O作OH⊥AC于点H.若OH=3,AB=8,BO=10.求:
(1)⊙O的半径;
(2)弦AC的长(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
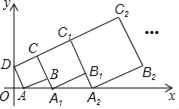
【题目】在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
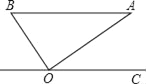
【题目】如图,在Rt△ABO中,斜边AB=1,若OC∥BA,∠AOC=36°,则( )
A. 点B到AO的距离为sin54°
B. 点A到OC的距离为sin36°sin54°
C. 点B到AO的距离为tan36°
D. 点A到OC的距离为cos36°sin54°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com