
【题目】如图,在Rt△ABO中,斜边AB=1,若OC∥BA,∠AOC=36°,则( )
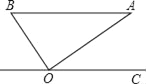
A. 点B到AO的距离为sin54°
B. 点A到OC的距离为sin36°sin54°
C. 点B到AO的距离为tan36°
D. 点A到OC的距离为cos36°sin54°
【答案】B
【解析】分析:过A作AD![]() OC,利用平行线性质可知∠A=∠AOC,所以可以解直角三角形,得到BO ,AO,再解直接三角形,可以得到A到OC的距离.
OC,利用平行线性质可知∠A=∠AOC,所以可以解直角三角形,得到BO ,AO,再解直接三角形,可以得到A到OC的距离.
详解:解:B到AO的距离是指BO的长,
∵AB∥OC,
∴∠BAO=∠AOC=36°,
∵在Rt△BOA中,∠BOA=90°,AB=1,
∴sin36°=![]() ,
,
∴BO=ABsin36°=sin36°,
故A、C选项错误;
过A作AD⊥OC于D,则AD的长是点A到OC的距离,
∵∠BAO=36°,∠AOB=90°,
∴∠ABO=54°,
∵sin36°=![]() ,
,
∴AD=AOsin36°,
∵sin54°=![]() ,
,
∴AO=ABsin54°,
∵AB=1,
∴AD=ABsin54°sin36°=1×sin54°sin36°=sin54°sin36°,
故B选项正确,D选项错误;
故选:B.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠α和∠β互补,且∠α<∠β,则下列表示∠α的余角的式子中:①90°﹣∠α;②∠β﹣90°;③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠β﹣∠α)其中正确的有( )
(∠β﹣∠α)其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
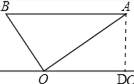
【题目】如图,已知四边形ABCD内接于⊙O,A是弧BDC的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且弧BF=弧AD.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,△ADF绕着点A顺时针旋转90°后得到△ABM,点M、B、C在一条直线上,且△AEM与△AEF恰好关于AE所在直线成轴对称。已知EF=7,正方形边长为8。

(1)写出图中形状、大小都相等的三角形
(2)求△EFC的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元![]() 与上网时间x(h)的函数关系如图所示,则下列判断错误的是
与上网时间x(h)的函数关系如图所示,则下列判断错误的是![]()
![]()
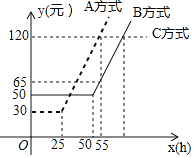
A. 每月上网时间不足25h时,选择A方式最省钱 B. 每月上网费用为60元时,B方式可上网的时间比A方式多
C. 每月上网时间为35h时,选择B方式最省钱 D. 每月上网时间超过70h时,选择C方式最省钱
查看答案和解析>>
科目:初中数学 来源: 题型:
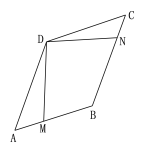
【题目】如图,边长为2的菱形ABCD中,∠A=60,点M是边AB上一点,点N是边BC上一点,且∠ADM=15,∠MDN=90,则点B到DN的距离为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元,设小明快递物品x千克.
(1)根据题意,填写下表:
快递物品重量(千克) | 0.5 | 1 | 3 | 4 | … |
甲公司收费(元) | 22 | … | |||
乙公司收费(元) | 11 | 51 | 67 | … |
(2)设甲快递公司收费y1元,乙快递公司收费y2元,分别写出y1,y2关于x的函数关系式;
(3)当x>3时,小明应选择哪家快递公司更省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )

A. AB∥DC,AD=BC B. AB∥DC,AD∥BC C. AB=DC,AD=BC D. OA=OC,OB=OD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com