
ЁОЬтФПЁПЯжДњЛЅСЊЭјММЪѕЕФЙуЗКгІгУЃЌДпЩњСЫПьЕнаавЕЕФИпЫйЗЂеЙЃЌаЁУїМЦЛЎИјХѓгбПьЕнвЛВПЗжЮяЦЗЃЌОСЫНтгаМзввСНМвПьЕнЙЋЫОБШНЯКЯЪЪ.МзЙЋЫОБэЪОЃКПьЕнЮяЦЗВЛГЌЙ§1ЧЇПЫЕФ,АДУПЧЇПЫ22дЊЪеЗбЃЛГЌЙ§1ЧЇПЫЃЌГЌЙ§ЕФВПЗжАДУПЧЇПЫ15дЊЪеЗбЃЌввЙЋЫОБэЪОЃКАДУПЧЇПЫ16дЊЪеЗбЃЌСэМгАќзАЗб3дЊЃЌЩшаЁУїПьЕнЮяЦЗxЧЇПЫ.
(1)ИљОнЬтвтЃЌЬюаДЯТБэЃК
ПьЕнЮяЦЗжиСПЃЈЧЇПЫЃЉ | 0.5 | 1 | 3 | 4 | Ё |
МзЙЋЫОЪеЗбЃЈдЊЃЉ | 22 | Ё | |||
ввЙЋЫОЪеЗбЃЈдЊЃЉ | 11 | 51 | 67 | Ё |
(2)ЩшМзПьЕнЙЋЫОЪеЗбy1дЊЃЌввПьЕнЙЋЫОЪеЗбy2дЊЃЌЗжБ№аДГіy1,y2ЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
(3)ЕБx>3ЪБЃЌаЁУїгІбЁдёФФМвПьЕнЙЋЫОИќЪЁЧЎЃПЧыЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉ11,19,52,67ЃЛЃЈ2ЃЉ![]() ЃЛy2=16x+3ЃЛЃЈ3ЃЉЕБ3ЃМxЃМ4ЪБЃЌаЁУїгІбЁдёввЙЋЫОЪЁЧЎЃЛЕБx=4ЪБЃЌСНМвЙЋЫОЗбгУвЛбљЃЛЕБxЃО4ЃЌаЁУїгІбЁдёМзЙЋЫОЪЁЧЎЃЎ
ЃЛy2=16x+3ЃЛЃЈ3ЃЉЕБ3ЃМxЃМ4ЪБЃЌаЁУїгІбЁдёввЙЋЫОЪЁЧЎЃЛЕБx=4ЪБЃЌСНМвЙЋЫОЗбгУвЛбљЃЛЕБxЃО4ЃЌаЁУїгІбЁдёМзЙЋЫОЪЁЧЎЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнМзЁЂввЙЋЫОЕФЪеЗбЗНЪНЃЌЧѓГіyжЕМДПЩЃЛ
ЃЈ2ЃЉИљОнМзЁЂввЙЋЫОЕФЪеЗбЗНЪННсКЯЪ§СПЙиЯЕЃЌевГіy1ЁЂy2ЃЈдЊЃЉгыxЃЈЧЇПЫЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉxЃО3ЃЌЗжБ№ЧѓГіy1ЃОy2ЁЂy1=y2ЁЂy1ЃМy2ЪБxЕФШЁжЕЗЖЮЇЃЌзлЩЯМДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉЕБx=0.5ЪБЃЌyМз=22ЁС0.5=11ЃЛ
ЕБx=1ЪБЃЌyвв=16ЁС1+3=19ЃЛ
ЕБx=3ЪБЃЌyМз=22+15ЁС2=52ЃЛ
ЕБx=4ЪБЃЌyМз=22+15ЁС3=67.
ЙЪД№АИЮЊЃК11ЃЛ19ЃЛ52ЃЛ67ЃЎ
ЃЈ2ЃЉЕБ0ЃМxЁм1ЪБЃЌy1=22xЃЛ
ЕБxЃО1ЪБЃЌy1=22+15ЃЈx-1ЃЉ=15x+7ЃЎ
Ёр ![]()
y2=16x+3ЃЈxЃО0ЃЉЃЛ
ЃЈ3ЃЉЕБxЃО3ЪБЃЌ
ЕБy1ЃОy2ЪБЃЌга15x+7ЃО16x+3ЃЌ
НтЕУЃКxЃМ4ЃЛ
ЕБy2=y2ЪБЃЌга15x+7=16x+3ЃЌ
НтЕУЃКx=4ЃЛ
ЕБy1ЃМy2ЪБЃЌга15x+7ЃМ16x+3ЃЌ
НтЕУЃКxЃО4ЃЎ
ЁрЕБ3ЃМxЃМ4ЪБЃЌаЁУїгІбЁдёввЙЋЫОЪЁЧЎЃЛЕБx=4ЪБЃЌСНМвЙЋЫОЗбгУвЛбљЃЛЕБxЃО4ЃЌаЁУїгІбЁдёМзЙЋЫОЪЁЧЎЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЫљЪОЕФЪЧДјжЇМмЙІФмЕФФГЦЗХЦЪжЛњПЧЃЌНЋЦфВрУцГщЯѓЮЊШчЭМ2ЫљЪОЕФМИКЮЭМаЮЃЌвбжЊAB=5cmЃЌЁЯBAC=60ЁуЃЌЁЯC=45ЁуЃЌдђACЕФГЄЃЈ![]() Ёж1.732ЃЌНсЙћОЋШЗЕН0.1cmЃЉЮЊЃЈЁЁЁЁЃЉ
Ёж1.732ЃЌНсЙћОЋШЗЕН0.1cmЃЉЮЊЃЈЁЁЁЁЃЉ
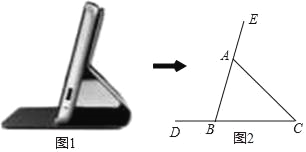
A. 3.4cm B. 4.6cm C. 5.8cm D. 6.8cm
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABOжаЃЌаББпAB=1ЃЌШєOCЁЮBAЃЌЁЯAOC=36ЁуЃЌдђЃЈЁЁЁЁЃЉ
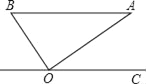
A. ЕуBЕНAOЕФОрРыЮЊsin54Ёу
B. ЕуAЕНOCЕФОрРыЮЊsin36Ёуsin54Ёу
C. ЕуBЕНAOЕФОрРыЮЊtan36Ёу
D. ЕуAЕНOCЕФОрРыЮЊcos36Ёуsin54Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊе§ЗНаЮABCDЕФБпГЄЮЊ4ЃЌЕуEЁЂFЗжБ№дкБпABЁЂBCЩЯЃЌЧвAE=BF=1ЃЌCEЁЂDFЯрНЛгкЕуOЃЌЯТСаНсТлЃК
ЂйЁЯDOC=90ЁуЃЌЂкOC=OEЃЌЂлtanЁЯOCD=![]() ЃЌЂмЁїCODЕФУцЛ§ЕШгкЫФБпаЮBEOFЕФУцЛ§ЃЌе§ШЗЕФга ЃЈЁЁЁЁЃЉ
ЃЌЂмЁїCODЕФУцЛ§ЕШгкЫФБпаЮBEOFЕФУцЛ§ЃЌе§ШЗЕФга ЃЈЁЁЁЁЃЉ
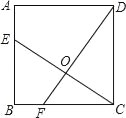
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЪ§жсЩЯСНЕуAЃЌBБэЪОЕФЪ§ЗжБ№ЮЊЉ2ЃЌ6ЃЌгУЗћКХЁАABЁБРДБэЪОЕуAКЭЕуBжЎМфЕФОрРыЃЎ
![]()
ЃЈ1ЃЉЧѓABЕФжЕЃЛ
ЃЈ2ЃЉШєдкЪ§жсЩЯДцдквЛЕуCЃЌЪЙACЃН3BCЃЌЧѓЕуCБэЪОЕФЪ§ЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕуCЮЛгкAЁЂBСНЕужЎМфЃЎЕуAвд1ИіЕЅЮЛ/УыЕФЫйЖШбизХЪ§жсЕФе§ЗНЯђдЫЖЏЃЌ2УыКѓЕуCвд2ИіЕЅЮЛ/УыЕФЫйЖШвВбизХЪ§жсЕФе§ЗНЯђдЫЖЏЃЌЕНДяBЕуДІСЂПЬЗЕЛибизХЪ§жсЕФИКЗНЯђдЫЖЏЃЌжБЕНЕуAЕНДяЕуBЃЌСНИіЕуЭЌЪБЭЃжЙдЫЖЏЃЎЩшЕуAдЫЖЏЕФЪБМфЮЊtЃЌдкДЫЙ§ГЬжаДцдкtЪЙЕУACЃН3BCШдГЩСЂЃЌЧѓtЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫугыМђЛЏЃК
ЃЈ1ЃЉЉ22Љ[ЃЈ1Љ1ЁС0.6ЃЉ+ЃЈЉ0.2ЃЉ2Љ4]
ЃЈ2ЃЉ![]() ЃЈ2a2Љ9bЃЉЉ3ЃЈЉ5a2Љ
ЃЈ2a2Љ9bЃЉЉ3ЃЈЉ5a2Љ![]() bЃЉЉ3b
bЃЉЉ3b
ЃЈ3ЃЉxЉ![]() ЃН
ЃН![]() +2
+2
ЃЈ4ЃЉ![]() ЃН
ЃН![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаРэЪ§Ъ§aЃЌbдкжсЩЯЕФБэЪОШчЭМЫљЪОЃЌдђЯТСаНсТлжаЃКЂйabЃМ0ЃЌЂкa+bЃМ0ЃЌЂлaЉbЃМ0ЃЌЂмaЃМ![]() ЃЌЂнЉaЃОЉbЃЌе§ШЗЕФгаЃЈ ЃЉ
ЃЌЂнЉaЃОЉbЃЌе§ШЗЕФгаЃЈ ЃЉ
![]()
A.2ИіB.3ИіC.4ИіD.5Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
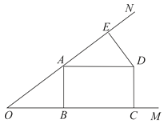
ЁОЬтФПЁПШчЭМЃЌЕуAдкЁЯMONЕФБпONЩЯЃЌABЁЭOMгкBЃЌAE=OBЃЌDEЁЭONгкEЃЌAD=AOЃЌDCЁЭOMгкCЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮABCDЪЧОиаЮЃЛ
ЃЈ2ЃЉШєDE=3ЃЌOE=9ЃЌЧѓABЁЂADЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк A ДІЙлВь C ВтЕУбіНЧЁЯCAD=31ЁуЃЌЧв AЁЂB ЕФЫЎЦНОрРы AE=800 УзЃЌаБЦТ AB ЕФЦТЖШi 1: 2 ЃЌЫїЕР BC ЕФЦТЖШi 2 : 3 ЃЌCDЁЭAD гк DЃЌBFЁЭCD гк FЃЌдђЫїЕРBC ЕФГЄДѓдМЪЧ( )
ЃЈВЮПМЪ§ОнЃКtan31ЁуЁж0. cos31ЁуЁж0.9ЃЌ![]() Ёж3.6ЃЉ
Ёж3.6ЃЉ

A. 1400 B. 1440 C. 1500 D. 1540
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com