
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标(4,2),过点D(0,3)和E(6,0)的直线分别于AB,BC交于点M,N.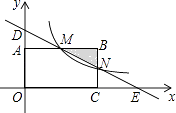
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数y= ![]() (x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
(x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
【答案】
(1)
解:设直线DE的解析式为y=kx+b,
∵D(0,3),E(6,0),
∴ ![]() ,解得
,解得 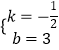 ,
,
∴直线DE的解析式为y=﹣ ![]() x+3;
x+3;
当y=2时,﹣ ![]() x+3=2,解得x=2,
x+3=2,解得x=2,
∴M的坐标为(2,2);
(2)
解:∵反比例函数y= ![]() (x>0)的图象经过点M(2,2),
(x>0)的图象经过点M(2,2),
∴m=2×2=4,
∴该反比函数的解析式是y= ![]() ;
;
∵直线DE的解析式为y=﹣ ![]() x+3,
x+3,
∴当x=4时,y=﹣ ![]() ×4+3=1,
×4+3=1,
∴N点坐标为(4,1),
∵4×1=4,
∴点N在函数y= ![]() 的图象上.
的图象上.
【解析】(1)设直线DE的解析式为y=kx+b,将D(0,3),E(6,0)代入,利用待定系数法求出直线DE的解析式;由矩形的性质可得M点与B点纵坐标相等,将y=2代入直线DE的解析式,求出x的值,即可得到M的坐标;(2)将点M(2,2)代入y= ![]() ,利用待定系数法求出反比函数的解析式,再由直线DE的解析式求出N点坐标,进而即可判断点N是否在该函数的图象上.
,利用待定系数法求出反比函数的解析式,再由直线DE的解析式求出N点坐标,进而即可判断点N是否在该函数的图象上.


科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的△ABC,若小方格边长为1,格点△ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别为(﹣1,1),(0,﹣2),请你根据所学的知识.

(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的三角形A1B1C1;
(3)判断△ABC的形状,并求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,BO,CO分别是∠ABC和∠ACB的平分线,过O点的直线分别交AB、AC于点D、E,且DE∥BC.若AB=6 cm,AC=8 cm,则△ADE的周长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(a,3),点P在坐标轴上,若使得△AOP是等腰三角形的点P恰有6个,则满足条件的a值有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一批单价为20元的商品,若每件按24元的价格销售时,每天能卖出36件;若每件按29元的价格销售时,每天能卖出21件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润P最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y1=x2﹣2x﹣1与反比例函数y2=﹣ ![]() (x>0)的图象在如图所示的同一坐标系中,若y1>y2时,则x的取值范围( )
(x>0)的图象在如图所示的同一坐标系中,若y1>y2时,则x的取值范围( )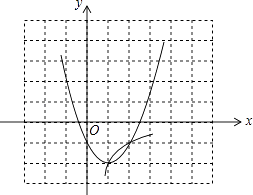
A.﹣1<x<1 或 x>2
B.1<x<2
C.x<1
D.0<x<1或x>2
查看答案和解析>>
科目:初中数学 来源: 题型:
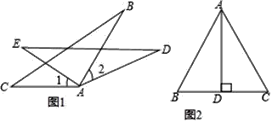
【题目】(1)如图1,AC=AE,∠1=∠2,∠C=∠E.求证:BC=DE.
(2)如图2,在△ABC中,AB=AC,D为BC中点,∠BAD=30°,求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )

A. 8 B. 16 C. 24 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(3x-2y)2-2x(3x-2y);
(2)(2a+1)(4a2-2a+1);
(3)先化简,再求值:
(-x-2y)(x-2y)-(2y-x)2+(2x3-4x2y)÷2x,其 中x=-3,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com