
【题目】如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,如图,A、B两点在函数y= ![]() (x>0)的图象上,则图中阴影部分(不包括边界)所含格点的个数为( )
(x>0)的图象上,则图中阴影部分(不包括边界)所含格点的个数为( ) 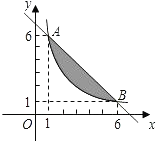
A.1
B.2
C.3
D.4
【答案】C
【解析】解:把A(1,6)代入y= ![]() ,得k=1×6=6, ∴反比例函数的解析式为y=
,得k=1×6=6, ∴反比例函数的解析式为y= ![]() ;
;
设直线AB的解析式为y=kx+b,
把A(1,6),B(6,1)代入得,kx+b=6,k+b=1,解得k=﹣1,b=7,
∴直线AB的解析式为y=﹣x+7;
当x=2,y= ![]() =3;y=﹣x+7=5;
=3;y=﹣x+7=5;
当x=3,y= ![]() =2;y=﹣x+7=4;
=2;y=﹣x+7=4;
当x=4,y= ![]() =
= ![]() ;y=﹣x+7=3;
;y=﹣x+7=3;
当x=5,y= ![]() =
= ![]() ;y=﹣x+7=2,
;y=﹣x+7=2,
∴图中阴影部分(不包括边界)所含格点的有:(2,4),(3,3),(4,2).
所以答案是C.
【考点精析】本题主要考查了反比例函数的性质的相关知识点,需要掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,有下列结论: ①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确的结论是 .
(把你认为正确结论的序号都填上)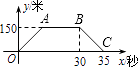
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD:AO=8:5,BC=3,求BD的长.
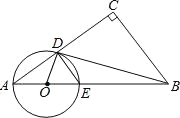
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形. 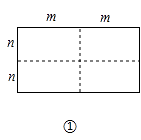
(1)图②中的阴影部分的正方形边长为; 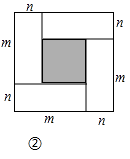
(2)观察图②,三个代数式(m+n)2 , (m﹣n)2 , mn之间的等量关系是; 
(3)观察图③,你能得到怎样的代数恒等式呢?; 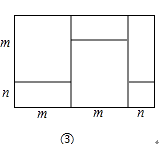
(4)试画出一个几何图形,使它的面积能表示(m+n)(m+2n)=m2+3mn+2n2 . (画在虚线框内)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
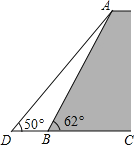
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2-(3m+2) x+2m+2=0(m>0).
(1)求证:方程有两个不相等的实数根且其中一个根为定值;
(2)设方程的两个实数根分别为x1、x2(其中x1<x2),若y是关于m的函数,且y=7x1-mx2,求这个函数的表达式;并求当自变量m的取值范围满足什么条件时,y≤3m.
查看答案和解析>>
科目:初中数学 来源: 题型:
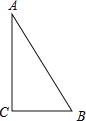
【题目】如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的面积;
(2)当t为几秒时,BP平分∠ABC;
(3)问t为何值时,△BCP为等腰三角形?
(4)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com