
【题目】已知关于x的一元二次方程mx2-(3m+2) x+2m+2=0(m>0).
(1)求证:方程有两个不相等的实数根且其中一个根为定值;
(2)设方程的两个实数根分别为x1、x2(其中x1<x2),若y是关于m的函数,且y=7x1-mx2,求这个函数的表达式;并求当自变量m的取值范围满足什么条件时,y≤3m.
【答案】(1)证明见解析;(2)y=-2m+5;当m≥1时,y≤3m.
【解析】试题分析:(1)先计算判别式的值得到△=(m+2)2,由m>0,得到△>0,根据判别式的意义得到方程有两个不相等的实数根,再利用求根公式得到x=![]() ,可得到方程有一个根为1,于是得到方程有两个不相等的实数根且其中一根为定值.
,可得到方程有一个根为1,于是得到方程有两个不相等的实数根且其中一根为定值.
(2)解方程得到x1=1,x2=2+![]() ,所以y=7-m(2+
,所以y=7-m(2+![]() )=-2m+5,然后解不等式-2m+5≤3m.
)=-2m+5,然后解不等式-2m+5≤3m.
试题解析:(1)证明:△=(3m+2)2-4m(2m+2)
=m2+4m+4
=(m+2)2,
∵m>0,
∴(m+2)2>0,即△>0,
∴方程有两个不相等的实数根,
∵x=![]() ,
,
∴方程有一个根为1,
∴方程有两个不相等的实数根且其中一根为定值.
(2)∵x=![]() ,
,
∴x1=1,x2=2+![]() ,
,
∴y=7x1-mx2
=7-m(2+![]() )
)
=-2m+5,
当y≤3m,即-2m+5≤3m,
∴m≥1.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
【题目】如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,如图,A、B两点在函数y= ![]() (x>0)的图象上,则图中阴影部分(不包括边界)所含格点的个数为( )
(x>0)的图象上,则图中阴影部分(不包括边界)所含格点的个数为( ) 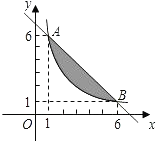
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程ax2+bx+c=0(a≠0).有下列命题:①若a+b+c=0,则b2-4ac≥0;②若一元二次方程ax2+bx+c=0的两根为-1和2,则2a+c=0;③若一元二次方程ax2+c=0有两个不相等的实数根,则一元二次方程ax2+bx+c=0必有两个不相等的实数根.其中真命题的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD的边AB=3,BC=4,点P是BC边上一动点(不与B、C重合),现将△ABP沿AP翻折,得到△AFP,再在CD边上选择适当的点E,将△PCE沿PE翻折,得到△PME,且直线PF、PM重合,若点F落在矩形纸片的内部,则CE的最大值是 .
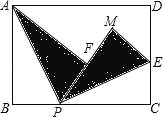
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】环境监测中PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如果1微米=0.000001米,那么数据0.0000025用科学记数法可以表示为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com