
ЁОЬтФПЁПвЛИБШ§НЧАхШчЭМ1АкЗХ,ЁЯC=ЁЯDFE=90,ЁЯB=30,ЁЯE=45,ЕуFдкBCЩЯ,ЕуAдкDFЩЯ,ЧвAFЦНЗжЁЯCAB,ЯжНЋШ§НЧАхDFEШЦЕуFЫГЪБеыа§зЊ(ЕБЕуDТфдкЩфЯпFBЩЯЪБЭЃжЙа§зЊ).
(1)ЕБЁЯAFD=_ __ЪБ,DFЁЮAC;ЕБЁЯAFD=__ _ЪБЃЌDFЁЭABЃЛ
(2)дка§зЊЙ§ГЬжаЃЌDFгыABЕФНЛЕуМЧЮЊPЃЌШчЭМ2ЃЌШєAFPгаСНИіФкНЧЯрЕШЃЌЧѓЁЯAPDЕФЖШЪ§ЃЛ
(3)ЕББпDEгыБпABЁЂBCЗжБ№НЛгкЕуMЁЂNЪБЃЌШчЭМ3ЃЌШєЁЯAFM=2ЁЯBMNЃЌБШНЯЁЯFMNгыЁЯFNMЕФДѓаЁЃЌВЂЫЕУїРэгЩЁЃ
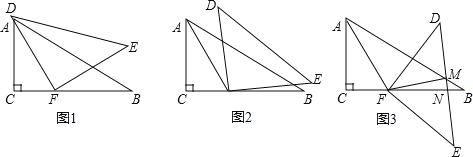
ЁОД№АИЁП(1)30ЃЛ60(2) 60Лђ105Лђ150(3)ЁЯFMN=ЁЯFNM
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉЕБЁЯAFD=30ЁуЪБЃЌACЁЮDFЃЌвРОнНЧЦНЗжЯпЕФЖЈвхПЩЯШЧѓЕУЁЯCAF=ЁЯFAB=30ЁуЃЌгЩФкДэНЧЯрЕШЃЌСНжБЯпЦНааЃЌПЩжЄУїACЁЮDFЃЌЃЛЕБЁЯAFD=60ЁуЪБЃЌDFЁЭABЃЌгЩШ§НЧаЮЕФФкНЧКЭЖЈРэжЄУїМДПЩЃЛ
ЃЈ2ЃЉЗжЮЊЁЯFAP=ЁЯAFPЃЌЁЯAFP=ЁЯAPFЃЌЁЯAPF=ЁЯFAPШ§жжЧщПіЧѓНтМДПЩЃЛ
ЃЈ3ЃЉЯШвРОнШ§НЧаЮЭтНЧЕФаджЪжЄУїЁЯFNM=30Ёу+ЁЯBMNЃЌНгЯТРДдйвРОнШ§НЧаЮЭтНЧЕФаджЪвдМАЁЯAFMКЭЁЯBMNЕФЙиЯЕПЩжЄУїЁЯFMN=30Ёу+ЁЯBMNЃЌДгЖјПЩЕУЕНЁЯFNMгыЁЯFMNЕФЙиЯЕЃЎ
ЯъНтЃКЃЈ1ЃЉШчЭМ1ЫљЪОЃК

ЕБЁЯAFD=30ЪБЃЌACЁЮDFЃЎ
РэгЩЃКЁпЁЯCAB=60ЁуЃЌAFЦНЗжЁЯCABЃЌЁрЁЯCAF=30ЁуЃЎ
ЁпЁЯAFD=30ЁуЃЌЁрЁЯCAF=ЁЯAFDЃЌЁрACЁЮDFЃЎ
ШчЭМ2ЫљЪОЃКЕБЁЯAFD=60ЁуЪБЃЌDFЁЭABЃЎ
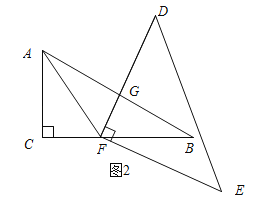
ЁпЁЯCAB=60ЁуЃЌAFЦНЗжЁЯCABЃЌЁрЁЯAFG=30ЁуЃЎ
ЁпЁЯAFD=60ЁуЃЌЁрЁЯFGB=90ЁуЃЌЁрDFЁЭABЃЎ
ЙЪД№АИЮЊЃК30ЃЛ60ЃЎ
ЃЈ2ЃЉЁпЁЯCAB=60ЁуЃЌAFЦНЗжЁЯCABЃЌЁрЁЯFAP=30ЁуЃЎ
ЕБШчЭМ3ЫљЪОЃК

ЕБЁЯFAP=ЁЯAFP=30ЁуЪБЃЌЁЯAPD=ЁЯFAP+ЁЯAFP=30Ёу+30Ёу=60ЁуЃЛ
ШчЭМ4ЫљЪОЃК

ЕБЁЯAFP=ЁЯAPFЪБЃЎ
ЁпЁЯFAP=30ЁуЃЌЁЯAFP=ЁЯAPFЃЌЁрЁЯAFP=ЁЯAPF=![]() ЁСЃЈ180ЁуЉ30ЁуЃЉ=
ЁСЃЈ180ЁуЉ30ЁуЃЉ=![]() ЁС150Ёу=75ЁуЃЌЁрЁЯAPD=ЁЯFAP+ЁЯAFP=30Ёу+75Ёу=105ЁуЃЛ
ЁС150Ёу=75ЁуЃЌЁрЁЯAPD=ЁЯFAP+ЁЯAFP=30Ёу+75Ёу=105ЁуЃЛ
ШчЭМ5ЫљЪОЃК
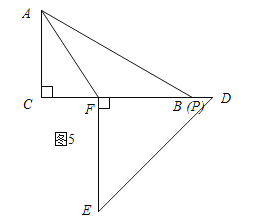
ШчЭМ5ЫљЪОЃКЕБЁЯAPF=ЁЯFAP=30ЁуЪБЃЎ
ЁЯAPD=180ЁуЉ30Ёу=150ЁуЃЎ
злЩЯЫљЪіЃКЁЯAPDЕФЖШЪ§ЮЊ60ЁуЛђ105ЁуЛђ150ЁуЃЎ
ЃЈ3ЃЉЁЯFMN=ЁЯFNMЃЎ
РэгЩЃКШчЭМ6ЫљЪОЃК
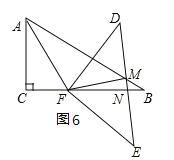
ЁпЁЯFNMЪЧЁїBMNЕФвЛИіЭтНЧЃЌЁрЁЯFNM=ЁЯB+ЁЯBMNЃЎ
ЁпЁЯB=30ЁуЃЌЁрЁЯFNM=ЁЯB+ЁЯBMN=30Ёу+ЁЯBMNЃЎ
ЁпЁЯBMFЪЧЁїAFMЕФвЛИіЭтНЧЃЌЁрЁЯMBF=ЁЯMAF+ЁЯAFMЃЌМДЁЯBMN+ЁЯFMN=ЁЯMAF+ЁЯAFMЃЎ
гжЁпЁЯMAF=30ЁуЃЌЁЯAFM=2ЁЯBMNЃЌЁрЁЯBMN+ЁЯFMN=30Ёу+2ЁЯBMNЃЌЁрЁЯFMN=30Ёу+ЁЯBMNЃЌЁрЁЯFNM=ЁЯFMNЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЮвУЧАбКсЁЂзнзјБъЖМЪЧећЪ§ЕФЕуНазіећЕуЃЌЧвЙцЖЈЃКе§ЗНаЮФкВП ВЛАќКЌБпНчЩЯЕФЕуЃЎЙлВьШчЭМЫљЪОЕФжааФдкдЕуЁЂвЛБпЦНаагк x жсЕФе§ЗНаЮЃКБпГЄЮЊ 1 ЕФе§ЗНаЮФкВПга 1 ИіећЕуЃЌБпГЄЮЊ 2 ЕФе§ЗНаЮФкВПга 1 ИіећЕуЃЌБпГЄЮЊ 3 ЕФе§ЗНаЮФкВП га 9 ИіећЕуЃЌЁЃЌдђБпГЄЮЊ 10 ЕФе§ЗНаЮФкЕФећЕуИіЪ§ЮЊЃЈ ЃЉ

A. 64 Иі B. 100 Иі C. 81 Иі D. 121 Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌEЪЧBCЕФжаЕуЃЌСЌНгAEВЂбгГЄНЛDCЕФбгГЄЯпгкЕуFЃЎ

ЃЈ1ЃЉЧѓжЄЃКAB=CFЃЛ
ЃЈ2ЃЉСЌНгDEЃЌШєAD=2ABЃЌЧѓжЄЃКDEЁЭAFЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєxЪЧЗНГЬ2x+mЉ3ЃЈmЉ1ЃЉЃН1+xЕФНтЮЊИКЪ§ЃЌдђmЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
A.mЃОЉ1B.mЃМЉ1C.mЃО1D.mЃМ1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌЕуEЃЌFдкЖдНЧЯпACЩЯЃЌЧвAE=CFЃЎЧѓжЄЃК
ЃЈ1ЃЉDE=BFЃЛ
ЃЈ2ЃЉЫФБпаЮDEBFЪЧЦНааЫФБпаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШБпЁїABCЕФБпГЄЪЧ2ЃЌDЁЂEЗжБ№ЮЊABЁЂACЕФжаЕуЃЌбгГЄBCжСЕуFЃЌЪЙCF=![]() BCЃЌСЌНгCDКЭEFЃЎ
BCЃЌСЌНгCDКЭEFЃЎ
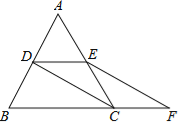
ЃЈ1ЃЉЧѓжЄЃКDE=CFЃЛ
ЃЈ2ЃЉЧѓEFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЁїABCЕФAЁЂBСНИіЖЅЕудкxжсЩЯЃЌЖЅЕуCдкyжсЕФИКАыжсЩЯЃЎвбжЊ|OA|ЃК|OB|=1ЃК5ЃЌ|OB|=|OC|ЃЌЁїABCЕФУцЛ§SЁїABC=15ЃЌХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉОЙ§AЁЂBЁЂCШ§ЕуЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЩшEЪЧyжсгвВрХзЮяЯпЩЯвьгкЕуBЕФвЛИіЖЏЕуЃЌЙ§ЕуEзїxжсЕФЦНааЯпНЛХзЮяЯпгкСэвЛЕуFЃЌЙ§ЕуFзїFGДЙжБгкxжсгкЕуGЃЌдйЙ§ЕуEзїEHДЙжБгкxжсгкЕуHЃЌЕУЕНОиаЮEFGHЃЎдђдкЕуEЕФдЫЖЏЙ§ГЬжаЃЌЕБОиаЮEFGHЮЊе§ЗНаЮЪБЃЌЧѓГіИУе§ЗНаЮЕФБпГЄЃЛ
ЃЈ3ЃЉдкХзЮяЯпЩЯЪЧЗёДцдквьгкBЁЂCЕФЕуMЃЌЪЙЁїMBCжаBCБпЩЯЕФИпЮЊ ![]() ЃПШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧыФуСаОйвЛИіПЩвдЭЈЙ§а§зЊЖјЕУЕНЕФМИКЮЬхЃК________________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ10ЗжЃЉдкЖЋгЊЪажааЁбЇБъзМЛЏНЈЩшЙЄГЬжаЃЌФГбЇаЃМЦЛЎЙКНјвЛХњЕчФдКЭЕчзгАзАхЃЌОЙ§ЪаГЁПМВьЕУжЊЃЌЙКТђ1ЬЈЕчФдКЭ2ЬЈЕчзгАзАхашвЊ3ЃЎ5ЭђдЊЃЌЙКТђ2ЬЈЕчФдКЭ1ЬЈЕчзгАзАхашвЊ2ЃЎ5ЭђдЊЃЎ
ЃЈ1ЃЉЧѓУПЬЈЕчФдЁЂУПЬЈЕчзгАзАхИїЖрЩйЭђдЊЃП
ЃЈ2ЃЉИљОнбЇаЃЪЕМЪЃЌашЙКНјЕчФдКЭЕчзгАзАхЙВ30ЬЈЃЌзмЗбгУВЛГЌЙ§30ЭђдЊЃЌЕЋВЛЕЭгк28ЭђдЊЃЌЧыФуЭЈЙ§МЦЫуЧѓГігаМИжжЙКТђЗНАИЃЌФФжжЗНАИЗбгУзюЕЭЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com