
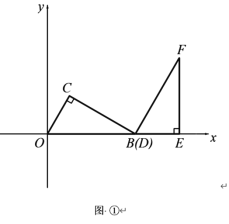
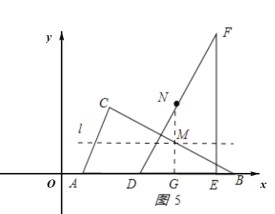
����Ŀ����ƽ��ֱ������ϵ�У�������״����С��ȫ��ͬ�����ǰ�OBC��DEF������ͼ��ʾ��λ�ðڷţ�OΪԭ�㣬��B(12��0) ����B���D�غϣ���OB���DE����x���ϣ����У���C=��DEF=90������OBC=��F=30����
��1����ͼ�������C���ꣻ
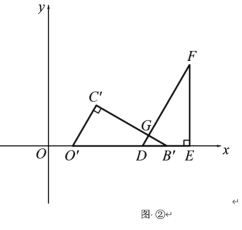
��2���̶ֹ����ǰ�DEF�������ǰ�OBC��x��������ƽ�ƣ��õ���O��B��C�� ������O�� ���D��ʱֹͣ�˶��������ǰ�ƽ�Ƶľ���Ϊx���������ǰ��ص����ֵ����Ϊy����y����x�ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
��3���ڣ�2�������£����BC���е�Ϊ��M����DF���е�Ϊ��N��ֱ��д�������ǰ�ƽ�ƹ����У�����M���N֮��ľ�����Сʱ����M�����ֱ꣨��д��������ɣ���
���𰸡���1��C (3 ,![]() )����2��
)����2�� ����3��M
����3��M ![]()
��������
��1������C��CG��AB��G�㣬����B(12��0) ����C=��DEF=90������OBC=��F=30������OB=12�� OC=6������OG=OCcos60����CG=OCsin60�����������ɵõ����ꣻ
��2���������ۣ��ٵ�![]() ʱ���ڵ�
ʱ���ڵ�![]() ʱ�����������ε������ʽ���г����̿ɵô𰸣�
ʱ�����������ε������ʽ���г����̿ɵô𰸣�
��3�����ݵ���ֱ�������е�������д��߶���̣���![]() ��
��![]() ��ʱ
��ʱ![]() ��̣����������ε���λ�ߣ��ɵ�
��̣����������ε���λ�ߣ��ɵ�![]() ��
��![]() �ij��������߶εĺͲ�ɵõ�M�����꣮
�ij��������߶εĺͲ�ɵõ�M�����꣮
�⣺��1����ͼ����ʾ������C��CG��AB��G�㣮
��B(12��0) ����OB=12��
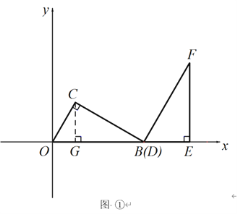
��Rt��OBC����OB=12����OBC=30������OC=6��
���COB=60��
��Rt��OCG��OG=OCcos60��=3��
��CG=OCsin60��=![]() ��
��
��C (3 ,![]() ).
).
��2������0��x��6ʱ����ͼ����ʾ��
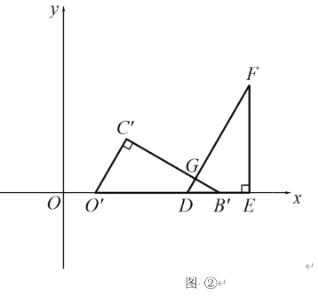
��GDE=60������GB��D=30����DB��=x����
DG=![]() ��B��G=
��B��G=![]() ���ص����ֵ����Ϊ
���ص����ֵ����Ϊ
y=![]() DGB��G=
DGB��G=![]()
![]() x
x![]()
����6��x��12ʱ����ͼ����ʾ��

B��D=x��DG=![]() x��B��G=
x��B��G=![]() ��B��E=x��6��
��B��E=x��6��
EH=![]() ��
��
�ص����ֵ����Ϊy=S��B��DG��S��B��EH=![]() DGB��G��
DGB��G��![]() B��EEH��
B��EEH��
��y=![]()
![]() x
x![]() -
-![]()
![]()
![]()
����y=![]() ��
��
���������� ��
��
��3����ͼ5��ʾ����![]() ��
��![]() �㣬
�㣬
��![]() ��
��![]() ��ʱ
��ʱ![]() ��̣�
��̣�
��![]() ��
��![]() ����λ�ߣ�
����λ�ߣ�
��![]() ��
��![]() ��
��
��![]() ��
��
��M��������![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ�ٱ�ʾһ��ʱ�ӵ����洹ֱ�̶���ˮƽ�����ϣ����з�������һ��A����������ʾ3��30��ʱ�����봹ֱ�����棬A�������ĸ߶�Ϊ10cm��ͼ�ڱ�ʾ��������ʾ3��45��ʱ��A�������ĸ߶�Ϊ16cm����������ʾ3��55��ʱ��A�������ĸ߶�Ϊ____![]() ��
��
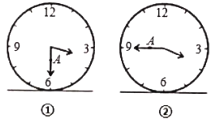
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2+bx+c��b��c�dz�������ͼ���㣨1����1����
��1���ú�b�Ĵ���ʽ��ʾc��
��2������κ���ͼ��Ķ�������������ֵ����д����ʱ���κ����ı���ʽ��
��3����ֱ��y���ֱ���루2�������õĶ��κ���ͼ���ڣ�x1��y1���ͣ�x2��y2������һ�κ���y=��x+2��ͼ���ڣ�x3��y3������x1<x2<x3����x1+x2+x3��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2020���¹ڷ��ױ�����ʡ����������֯ҽ����Ա�ͷ���ҩƷ�ϸ�������Ԯ��װ�ط���ҩƷ�Ļ��˷ɻ��ӻ�����������600ǧ��/Сʱ���ٶȷ��У���Сʱ��ҽ����Ա�������˷ɻ���ͬһ���������������˷ɻ��ٶ��ǻ��˷ɻ��ٶȵ�1.2����������˷ɻ���װ�ط���ҩƷ�Ļ��˷ɻ���15���ӵ��������
��1������˷ɻ�ȫ�̷���ʱ��ΪtСʱ����t��ʾ�����Ļ�����������·��s��
��2��������Ļ�����������·�̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
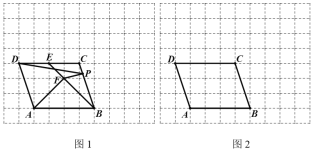
����Ŀ����ͼ1����ÿ��С�����εı߳�Ϊ1�������У���A��B��C��D���ڸ���ϣ���EΪֱ��CD�ϵĶ��㣬����BE����AF��BE��F����PΪBC���ϵĶ��㣬����DP��PF��
������EΪCD�ߵ��е�ʱ����ABF�����Ϊ ��
����DP��PF���ʱ������ͼ2��ʾ�������У����̶ȵ�ֱ������P������Ҫ˵����P��λ��������ҵ��ģ���Ҫ��֤�������� ���������������������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y��![]() .
.
(1)���÷�����������ͼ����ֱ��y��kx��4(k��0)ֻ��һ�������㣬��k��ֵ��
(2)��ͼ������������y��![]() (1��x��4)��ͼ���Ϊ����C1����C1����ƽ��2����λ���ȣ�������C2������ͼ�л���C2����ֱ��д��C1ƽ�Ƶ�C2����ɨ���������
(1��x��4)��ͼ���Ϊ����C1����C1����ƽ��2����λ���ȣ�������C2������ͼ�л���C2����ֱ��д��C1ƽ�Ƶ�C2����ɨ���������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c��a��0�Գ���Ϊֱ��x��1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ���abc��0����4ac��b2���۷���ax2+bx+c��0����������x1����1��x2��3����3a+c��0���ݵ�y��0ʱ��x��ȡֵ��Χ�ǩ�1��x��3�����н�����ȷ�ĸ����ǣ�������
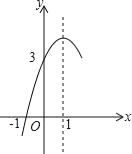
A. 1��B. 2��C. 3D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ƽ��ֱ������ϵ�У��ı���ABCD�����Σ�����B��������(8��2)��D��������(0��2)����A��x���ϣ�������ABCD���ܳ��ǣ� ��
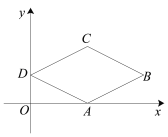
A.2![]()
B.8
C.8![]()
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
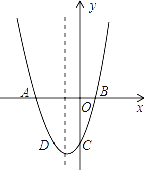
����Ŀ����12�֣���֪�����κ���y=x2+bx+c��ͼ����x�ύ��A��B���㣬����A������Ϊ����3��0������y�ύ�ڵ�C����D����2����3�����������ϣ�
��1���������ߵĽ���ʽ��
��2�������ߵĶԳ�������һ����P�����PA+PD����Сֵ��
��3��������������һ����P��ʹ������ABP�����Ϊ6����P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com