练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．如图，在一块长为60m，宽40m的矩形荒地正中央挖一块与荒地长度比例相同的矩形水池，要使水池面积是原荒地面积的$\frac{1}{4}$，上下荒地等宽，左右荒地等宽，求四周剩余荒地的宽度．

    分析 首先设上下荒地的宽度为3xm，则左右荒地的宽度为2xm，根据水池面积是原荒地面积的$\frac{1}{4}$，表示出水池面积即可得出等式方程．

    解答 解：设上下荒地的宽度为3xm，则左右荒地的宽度为2xm，依题意有
    （60-6x）（40-4x）=60×40×$\frac{1}{4}$，
    解得：x1=15（不合题意舍去），x2=5，
    3x=15，
    2x=10．
    答：上下荒地的宽度为15m，左右荒地的宽度为10m．

    点评 本题主要考查了一元二次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件水池面积是原荒地面积的$\frac{1}{4}$，列出方程即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    1．计算：$\sqrt{2}-\sqrt{6}×\sqrt{3}$=-2$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

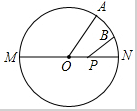    2．如图，MN是⊙0的直径，MN=2，点A在⊙0上，$\widehat{AON}$=60°，点B为$\widehat{AON}$的中点，点P是直径MN上的一个动点，则PA+PB的最小值为$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

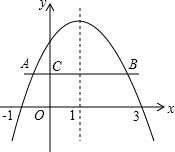    19．已知二次函数y=ax2+bx+c的图象如图所示，对称轴为直线x=1，点A、B是二次函数图象上的两点，AB∥x轴且与y轴交于点C（点C在二次函数图象于y轴交点的下方），有下列结论：①ac＜0；②方程ax2+bx+c=0的两根是x1=-1，x2=3；③函数有最小值，最小值是a+b+c；④当x＞0时，y随x的增大而减小；⑤BC=3AC．其中正确的结论的序号是①、②．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知α，β都是锐角，且cosβ+sinα=1.1176，cosβ-sinα=0.0580，则α≈32°，β≈54°．（结果保留整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

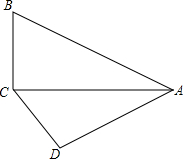    16．如图，在△ABC与△ACD中，∠ACB=∠ADC=90°，∠BAC=∠CAD=30°，则$\frac{{S}_{△ABC}}{{S}_{△ACD}}$=$\frac{4}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，已知△ABC中，AB＞AC．求证：∠C＞∠B．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．下列代数式-$\frac{1}{2}$a，0，$\frac{-m+2}{12}$，π，$\frac{1}{x}$，$\frac{p?}{3}$中，单项式个数有（　　）
    A．3个B．4个C．5个D．6个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．青春商场经销甲、乙两种商品，甲种商品每件进价20元，售价26元；乙种商品每件售价45元，利润为50%．
    （1）若该商场同时购进甲、乙两种商品共100件，恰好总进价用去2600元，求购进的甲商品多少件？
    （2）在“元旦”期间，该商场对甲、乙两种商品进行如下的优惠促销活动：
    打折前一次性购物总金额优惠措施
    不超过300元不优惠
    超过300元且不超过400元售价打九折
    超过400元售价打八折
    按上述优惠条件，若小聪第一天只购买甲种商品实际付款260元，第二天只购买乙种商品实际付款324元，求小聪这两天在该商场购买甲、乙两种商品一共多少件？

    查看答案和解析>>

    同步练习册答案