
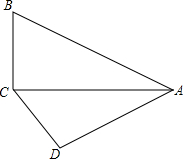
 如图,在△ABC与△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD=30°,则$\frac{{S}_{△ABC}}{{S}_{△ACD}}$=$\frac{4}{3}$.
如图,在△ABC与△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD=30°,则$\frac{{S}_{△ABC}}{{S}_{△ACD}}$=$\frac{4}{3}$. 分析 由于∠ACB=90°,∠BAC=30°,于是得到$\frac{AC}{AB}$=cos30°=$\frac{\sqrt{3}}{2}$,根据已知条件得到△ABC∽△ACD,然后根据相似三角形的性质即可得到结论.
解答 解:∵∠ACB=90°,∠BAC=30°,
∴$\frac{AC}{AB}$=cos30°=$\frac{\sqrt{3}}{2}$,
∴AC=$\frac{\sqrt{3}}{2}$AB,
∵∠ACB=∠ADC=90°,∠BAC=∠CAD=30°,
∴△ABC∽△ACD,
∴$\frac{{S}_{△ABC}}{{S}_{△ACD}}$=($\frac{AB}{AC}$)2=$\frac{4}{3}$,
故答案为:$\frac{4}{3}$.
点评 本题考查了解直角三角形,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
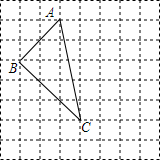 在如图所示的正方形网格中,格点三角形ABC(即顶点都是网格线的交点)的顶点A、C的坐标为A(-1,4)、B(-3,2).
在如图所示的正方形网格中,格点三角形ABC(即顶点都是网格线的交点)的顶点A、C的坐标为A(-1,4)、B(-3,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一块长为60m,宽40m的矩形荒地正中央挖一块与荒地长度比例相同的矩形水池,要使水池面积是原荒地面积的$\frac{1}{4}$,上下荒地等宽,左右荒地等宽,求四周剩余荒地的宽度.
如图,在一块长为60m,宽40m的矩形荒地正中央挖一块与荒地长度比例相同的矩形水池,要使水池面积是原荒地面积的$\frac{1}{4}$,上下荒地等宽,左右荒地等宽,求四周剩余荒地的宽度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
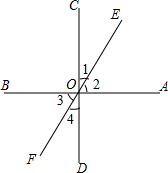 如图所示,三条直线AB,CD,EF都经过点O,且∠AOC=90°
如图所示,三条直线AB,CD,EF都经过点O,且∠AOC=90°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
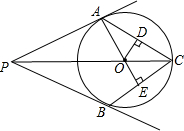 从⊙O外一点P引⊙O的切线PA、PB,切点分别为A、B两点,连结PO并延长PO交⊙O于点C,连接CA,CB,OD⊥AC,OE⊥CB,垂足分别为D、E,求证:OD=OE.
从⊙O外一点P引⊙O的切线PA、PB,切点分别为A、B两点,连结PO并延长PO交⊙O于点C,连接CA,CB,OD⊥AC,OE⊥CB,垂足分别为D、E,求证:OD=OE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com