
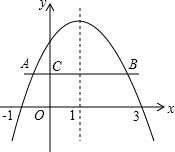
 已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,点A、B是二次函数图象上的两点,AB∥x轴且与y轴交于点C(点C在二次函数图象于y轴交点的下方),有下列结论:①ac<0;②方程ax2+bx+c=0的两根是x1=-1,x2=3;③函数有最小值,最小值是a+b+c;④当x>0时,y随x的增大而减小;⑤BC=3AC.其中正确的结论的序号是①、②.
已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,点A、B是二次函数图象上的两点,AB∥x轴且与y轴交于点C(点C在二次函数图象于y轴交点的下方),有下列结论:①ac<0;②方程ax2+bx+c=0的两根是x1=-1,x2=3;③函数有最小值,最小值是a+b+c;④当x>0时,y随x的增大而减小;⑤BC=3AC.其中正确的结论的序号是①、②. 分析 由抛物线的开口方向可确定a的符号,由抛物线与y轴的交点位置可确定c的符号,从而可以判定ac的符号;由抛物线与x轴交点坐标可得到方程ax2+bx+c=0的两根;由抛物线的开口方向可判定函数有最大值或最小值;结合图象可知二次函数的增减性;可举反例说明BC=3AC不一定正确.
解答 解:由抛物线的开口向下可得a<0,
由抛物线与y轴的交点在y轴的正半轴上可得c>0,
∴ac<0,故①正确;
由抛物线的与x轴的交点的横坐标分别为-1和3可得,
y=0即ax2+bx+c=0时,x1=-1,x2=3,故②正确;
由对称轴x=1及a<0可得,
当x=1时,函数有最大值,最大值是a+b+c,故③错误;
结合图象可得:
当0<x<1时,y随x的增大而增大;当x>1时,y随x的增大而减小,故④错误.
当a=-1,C(0,-5)时,抛物线的解析式为y=-(x+1)(x-3),
令y=-5,得-(x+1)(x-3)=-5,
整理得x2-2x-8=0,
解得x1=-2,x2=4,
此时AC=2,BC=4,
可得BC=2AC,故⑤错误.
综上所述:①、②正确.
故答案为①、②.
点评 本题主要考查二次函数图象与系数的关系、二次函数的性质等知识,其中a决定于抛物线的开口方向,c决定于抛物线与y轴的交点位置,抛物线与x轴交点横坐标就是方程ax2+bx+c=0的两根,运用数形结合的思想准确获取相关信息是解决本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
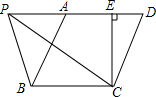 如图,?ABCD中,BC=5cm,CD=6cm,CE⊥AD于点E,CE=4cm,P为直线AD上一点.求;
如图,?ABCD中,BC=5cm,CD=6cm,CE⊥AD于点E,CE=4cm,P为直线AD上一点.求;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
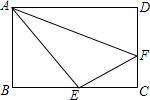 如图,在矩形ABCD中,点E为BC的中点,点F在CD上,要使△AEF的周长最小时,确定点F的位置的方法为作点E关于DC的对称点E′,连接AE′交CD于点F.
如图,在矩形ABCD中,点E为BC的中点,点F在CD上,要使△AEF的周长最小时,确定点F的位置的方法为作点E关于DC的对称点E′,连接AE′交CD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一块长为60m,宽40m的矩形荒地正中央挖一块与荒地长度比例相同的矩形水池,要使水池面积是原荒地面积的$\frac{1}{4}$,上下荒地等宽,左右荒地等宽,求四周剩余荒地的宽度.
如图,在一块长为60m,宽40m的矩形荒地正中央挖一块与荒地长度比例相同的矩形水池,要使水池面积是原荒地面积的$\frac{1}{4}$,上下荒地等宽,左右荒地等宽,求四周剩余荒地的宽度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
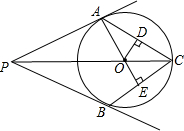 从⊙O外一点P引⊙O的切线PA、PB,切点分别为A、B两点,连结PO并延长PO交⊙O于点C,连接CA,CB,OD⊥AC,OE⊥CB,垂足分别为D、E,求证:OD=OE.
从⊙O外一点P引⊙O的切线PA、PB,切点分别为A、B两点,连结PO并延长PO交⊙O于点C,连接CA,CB,OD⊥AC,OE⊥CB,垂足分别为D、E,求证:OD=OE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com