
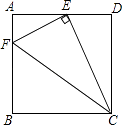
【题目】如图,在正方形ABCD中,点E为AD的中点,连接EC,过点E作EF⊥EC,交AB于点F,则tan∠ECF= . 
【答案】![]()
【解析】解:∵四边形ABCD是正方形, ∴AD=DC,∠A=∠D=90°,
∵AE=ED,
∴CD=AD=2AE,
∵∠FEC=90°,
∴∠AEF+∠DEC=90°,
∵∠DEC+∠DCE=90°,
∴∠AEF=∠DCE,∵∠A=∠D,
∴△AEF∽△DCE,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴tan∠ECF= ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考点精析】通过灵活运用正方形的性质和锐角三角函数的定义,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数即可以解答此题.


科目:初中数学 来源: 题型:
【题目】宁波火车站北广场将于2015年底投入使用,计划在广场内种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC三边长a=b=6![]() ,c=12.
,c=12.
(1)如图1,以点A为原点,AB所在直线为x轴建立平面直角坐标系,直接出点B,C的坐标.
(2)如图2,过点C作∠MCN=45°交AB于点M,N,请证明AM2+BN2=MN2;
(3)如图3,当点M,N分布在点B异侧时,则(3)中的结论还成立吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2、中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为( ) 
A.3
B.4﹣ ![]()
C.4
D.6﹣2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行抽样调查,结果统计如下,其中扇形统计图中C组所在的扇形的圆心角为36° 被抽取的体育测试成绩频数分布表
组别 | 成绩 | 频数 |
A | 20<x≤24 | 2 |
B | 24<x≤28 | 3 |
C | 28<x≤32 | 5 |
D | 32<x≤36 | b |
E | 36<x≤40 | 20 |
合计 | a | |
根据上面的图表提供的信息,回答下列问题: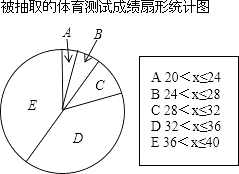
(1)计算频数分布表中a与b的值;
(2)根据C组28<x≤32的组中值30,估计C组中所有数据的和为;
(3)请估计该校九年级学生这次体育测试成绩的平均分(结果取整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,l1和l2分别是走私船和我公安快艇航行路程与时间的函数图象,请结合图象解决下列问题:
(1)在刚出发时,我公安快艇距走私船多少海里?
(2)计算走私船与公安艇的速度分别是多少?
(3)求出l1,l2的解析式.
(4)问6分钟时,走私船与我公安快艇相距多少海里?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,以点A为圆心,AB长为半径画弧,交CD于点E,连接AE、BE.作BF⊥AE于点F. 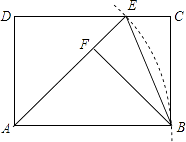
(1)求证:BF=AD;
(2)若EC= ![]() ﹣1,∠FEB=67.5°,求扇形ABE的面积(结果保留π).
﹣1,∠FEB=67.5°,求扇形ABE的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞架所成的角∠BAC,当伞收紧时,结点D与点M重合,且点A、E、D在同一条直线上,已知部分伞架的长度如下:单位:cm
伞架 | DE | DF | AE | AF | AB | AC |
长度 | 36 | 36 | 36 | 36 | 86 | 86 |
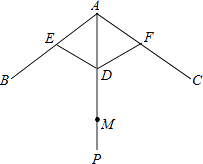
(1)求AM的长.
(2)当∠BAC=104°时,求AD的长(精确到1cm). 备用数据:sin52°=0.788,cos52°=0.6157,tan52°=1.2799.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
某校初二年级的同学乘坐大巴车去北京展览馆参观“砥砺奋进的五年”大型成就展,北京展览馆距离该校12千米,1号车出发3分钟后,2号车才出发,结果两车同时到达,已知2号车的平均速度是1号车的平均速度的1.2倍,求2号车的平均速度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com