
【题目】已知△ABC三边长a=b=6![]() ,c=12.
,c=12.
(1)如图1,以点A为原点,AB所在直线为x轴建立平面直角坐标系,直接出点B,C的坐标.
(2)如图2,过点C作∠MCN=45°交AB于点M,N,请证明AM2+BN2=MN2;
(3)如图3,当点M,N分布在点B异侧时,则(3)中的结论还成立吗?

【答案】(1)点C的坐标为(6,6);(2)见解析;(3)仍然成立.
【解析】
(1)利用勾股定理逆定理判断出是直角三角形,从而得到△ABC是等腰直角三角形,再根据等腰直角三角形的性质求出点C的横坐标与纵坐标即可得解;
(2)把△ACM绕点C逆时针旋转90°得到△BCM′,连接M′N,根据旋转的性质可得AM=BM′、CM=CM′、∠CAM=∠CBM′,∠ACM=∠BCM′,然后求出∠MCN=∠M′CN,∠M′BN=90°,再利用“边角边”证明△MCN和△M′CN全等,根据全等三角形对应边相等可得MN=M′N,然后利用勾股定理列式证明即可;
(3)把△BCN绕点C顺时针旋转90°得到△ACN′,根据旋转的性质可得AN′=BN,CN′=CN,∠CAN′=∠CBN,然后判断出点N′在y轴上,再求出∠MCN′=45°,从而得到∠MCN=∠MCN′,再利用“边角边”证明△MCN和△MCN′全等,根据全等三角形对应边相等可得MN=MN′,然后利用勾股定理列式即可得证.
(1)∵a=b=6![]() ,c=12,
,c=12,
∵a2+b2=(6![]() )2+(6
)2+(6![]() )2=144=c2,
)2=144=c2,
∴△ABC是直角三角形,
又∵a=b,
∴△ABC是等腰直角三角形;
∵AB=c=12,
∴点B(12,0),
如图1,过点C作CD⊥x轴于D,
则AD=CD=![]() AB=
AB=![]() ×12=6,
×12=6,
∴点C的坐标为(6,6);
(2)如图,把△ACM绕点C逆时针旋转90°得到△BCM′,连接M′N,
由旋转的性质得,AM=BM′、CM=CM′、∠CAM=∠CBM′=45°,∠ACM=∠BCM′,
∴∠M′BN=∠ABC+∠CBN′=45°+45°=90°,
∵∠MCN=45°,
∴∠M′CN=∠BCN+∠BCM′=∠BCN+∠ACM=90°﹣∠MCN=90°﹣45°=45°,
∴∠MCN=∠M′CN,
在△MCN和△M′CN中,
∵ ,
,
∴△MCN≌△M′CN(SAS),
∴MN=M′N,
在Rt△M′NB中,BM′2+BN2=M′N2,
∴AM2+BN2=MN2;
(3)仍然成立,
如图3,∵△ABC是等腰直角三角形,
∴∠CAB=∠CBA=45°,
把△BCN绕点C顺时针旋转90°得到△ACN′,
由旋转的性质得,AN′=BN,CN′=CN,∠CAN′=∠CBN=135°,
∴∠MAN′=135°﹣45°=90°,
∴点N′在y轴上,
∵∠MCN=45°,
∴∠MCN′=90°﹣45°=45°,
∴∠MCN=∠MCN′,
在△MCN和△MCN′中,
∵ ,
,
∴△MCN≌△MCN′(SAS),
∴MN=MN′,
在Rt△AMN′中,AM2+AN′2=MN′2,
∴AM2+BN2=MN2.


科目:初中数学 来源: 题型:
【题目】山西绵山是中国历史文化名山,因春秋时期晋国介子推携母隐居于此被焚而著称,如图1,是绵山上介子推母子的塑像,某游客计划测量这座塑像的高度,由于游客无法直接到达塑像底部,因此该游客计划借助坡面高度来测量塑像的高度;如图2,在塑像旁山坡坡脚A处测得塑像头顶C的仰角为75°,当从A处沿坡面行走10米到达P处时,测得塑像头顶C的仰角刚好为45°,已知山坡的坡度i=1:3,且O,A,B在同一直线上,求塑像的高度.(侧倾器高度忽略不计,结果精确到0.1米,参考数据:cos75°≈0.3,tan75°≈3.7, ![]() ≈1.4,
≈1.4, ![]() ≈1.7,
≈1.7, ![]() ≈3.2)
≈3.2)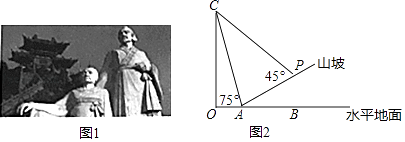
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中的数阵是由全体正奇数排成的.
(1)图中平行四边形框内的九个数之和与中间的数有什么关系?
(2)在图中任意作一个类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由.这九个数之和能等于2 016吗?2 015,2 025呢?若能,请写出这九个数中最小的一个;若不能,请说出理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在义乌市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为:“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图. 
请你结合图中信息,解答下列问题:
(1)本次共调查了名学生;
(2)被调查的学生中,最喜爱丁类图书的学生有人,最喜爱甲类图书的人数占本次被调查人数的%;
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(﹣2,0),(﹣1,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
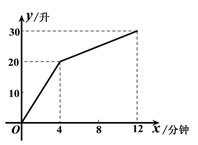
【题目】一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图象所示.求从关闭进水管起需要多少分钟该容器内的水恰好放完.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com