
【题目】计算:
(1)(﹣1)2015+(﹣ ![]() )﹣1+
)﹣1+ ![]() ﹣2sin45°.
﹣2sin45°.
(2)解不等式 ![]() ,并写出不等式的正整数解.
,并写出不等式的正整数解.
【答案】
(1)解:原式=﹣1﹣3+ ![]() ﹣
﹣ ![]() =﹣4
=﹣4
(2)解:去分母得:3x﹣3≤2x﹣1,
解得:x≤2,
则不等式的正整数解为1,2
【解析】(1)原式利用乘方的意义,负整数指数幂法则,绝对值的代数意义,以及特殊角的三角函数值计算即可得到结果;(2)不等式去分母,去括号,移项合并,把x系数化为1,求出解集,找出解集的正整数解即可.
【考点精析】本题主要考查了整数指数幂的运算性质和一元一次不等式的解法的相关知识点,需要掌握aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数);步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波火车站北广场将于2015年底投入使用,计划在广场内种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD的对角线AC,BD相交于点O,AC=4 ![]() ,BD=4,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为S1 , 未被盖住部分的面积为S2 , BP=x.
,BD=4,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为S1 , 未被盖住部分的面积为S2 , BP=x. 
(1)用含x的代数式分别表示S1 , S2;
(2)若S1=S2 , 求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列做法正确的是( )
A. 方程![]() =1+
=1+![]() 去分母,得2(2x-1)=1+3(x-3)
去分母,得2(2x-1)=1+3(x-3)
B. 方程4x=7x-8移项,得4x-7x=8
C. 方程3(5x-1)-2(2x-3)=7去括号,得15x-3-4x-6=7
D. 方程1-![]() x=3x+
x=3x+![]() 移项,得-
移项,得-![]() x-3x=
x-3x=![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2 , 垂足为D,过点O,B的直线l4交l2于点E,当直线l1 , l2 , l3能围成三角形时,设该三角形面积为S1 , 当直线l2 , l3 , l4能围成三角形时,设该三角形面积为S2 . 
(1)若点B在线段AC上,且S1=S2 , 则B点坐标为;
(2)若点B在直线l1上,且S2= ![]() S1 , 则∠BOA的度数为 .
S1 , 则∠BOA的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC三边长a=b=6![]() ,c=12.
,c=12.
(1)如图1,以点A为原点,AB所在直线为x轴建立平面直角坐标系,直接出点B,C的坐标.
(2)如图2,过点C作∠MCN=45°交AB于点M,N,请证明AM2+BN2=MN2;
(3)如图3,当点M,N分布在点B异侧时,则(3)中的结论还成立吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2、中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为( ) 
A.3
B.4﹣ ![]()
C.4
D.6﹣2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞架所成的角∠BAC,当伞收紧时,结点D与点M重合,且点A、E、D在同一条直线上,已知部分伞架的长度如下:单位:cm
伞架 | DE | DF | AE | AF | AB | AC |
长度 | 36 | 36 | 36 | 36 | 86 | 86 |
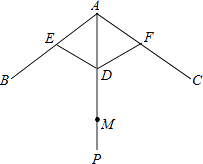
(1)求AM的长.
(2)当∠BAC=104°时,求AD的长(精确到1cm). 备用数据:sin52°=0.788,cos52°=0.6157,tan52°=1.2799.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com