
【题目】计算与化简
(1)-18+21+(-13)
(2)-81÷![]() ×
×![]() ÷(-16)
÷(-16)
(3)(![]() +
+![]() -
-![]() )×(-24)
)×(-24)
(4)-22-![]() ×[4-(-3)2]
×[4-(-3)2]
(5)化简:5(3x2y-xy2)-4(-xy2+2x2y)
(6)先化简,再求值:-![]() x+2(x-
x+2(x-![]() y2) - (-
y2) - (-![]() x+
x+![]() y2);其中x=2,y=
y2);其中x=2,y=![]() .
.
【答案】(1)-10;(2) 1 ;(3)-18 ;(4)-2 ; (5) 7x2y—xy2; (6) 3x—y2 ,5
【解析】
(1)根据有理数的加减运算法则计算即可得出答案;
(2)根据有理数的乘除运算法则计算即可得出答案;
(3)先去括号,再根据有理数的四则运算法则计算即可得出答案;
(4)先算乘方,再根据有理数的四则运算法则计算即可得出答案;
(5)先去括号,再根据整式的加减运算法则计算即可得出答案;
(6)先去括号,再利用整式的加减运算法则化简,最后将x和y的值代入计算即可得出答案.
(1)解:原式=-18+21-13
=-31+21
=-10.
(2)解:原式=![]()
= 1
(3)解:原式=![]()
=-18
(4)解:原式=-4-![]() ×﹙4-9﹚
×﹙4-9﹚
=-4-![]() ×﹙-5﹚
×﹙-5﹚
=-4+2
=-2
(5) 解:原式=![]()
= 7x2y—xy2
(6) 解:原式=![]()
=3x—y2
当![]() =2,
=2,![]() =
=![]() 时,
时,
原式=3×2-(-1)2
=5


科目:初中数学 来源: 题型:
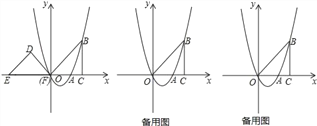
【题目】如图,抛物线y=ax2+bx(a≠0)经过点A(2,0),点B(3,3),BC⊥x轴于点C,连接OB,等腰直角三角形DEF的斜边EF在x轴上,点E的坐标为(﹣4,0),点F与原点重合
(1)求抛物线的解析式并直接写出它的对称轴;
(2)△DEF以每秒1个单位长度的速度沿x轴正方向移动,运动时间为t秒,当点D落在BC边上时停止运动,设△DEF与△OBC的重叠部分的面积为S,求出S关于t的函数关系式;
(3)点P是抛物线对称轴上一点,当△ABP是直角三角形时,请直接写出所有符合条件的点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
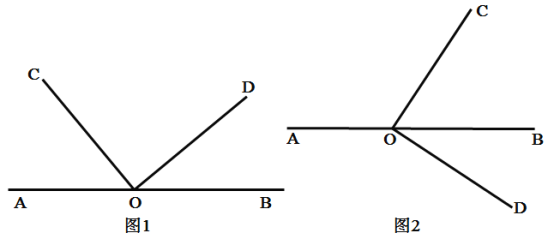
【题目】如图,点O是直线AB上的一点,OD⊥OC,过点O作射线OE平分∠BOC.
(1)如图1,如果∠AOC=50°,依题意补全图形,写出求∠DOE度数的思路(不需要写出完整的推理过程);
(2)当OD绕点O顺时针旋转一定的角度得到图2,使得直角边OC在直线AB的上方,若∠AOC=α,其他条件不变,依题意补全图形,并求∠DOE的度数(用含α的代数式表示);
(3)当OD绕点O继续顺时针旋转一周,回到图1的位置,在旋转过程中你发现∠AOC与∠DOE(0°≤∠AOC≤180°,0°≤∠DOE≤180°)之间有怎样的数量关系?请直接写出你的发现.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设![]() ,
,![]() ,
,![]() ,请探索
,请探索![]() ,
,![]() ,
,![]() 满足的等量关系。
满足的等量关系。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两站相距480千米,一辆快车从甲站出发,每小时行驶120千米,一辆慢车从乙站出发,每小时行驶80千米.
(1)两车同时开出,相向而行,多少小时后两车相遇?
(2)两车同时开出,相向而行,多少小时后两车相距100千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
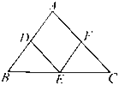
【题目】如图,在![]() 中,点
中,点![]() 分别是
分别是![]() 的中点,则下列四个判断中不一定正确的是()
的中点,则下列四个判断中不一定正确的是()
A. 四边形![]() 一定是平行四边形
一定是平行四边形
B. 若![]() ,则四边形
,则四边形![]() 是矩形
是矩形
C. 若四边形![]() 是菱形,则
是菱形,则![]() 是等边三角形
是等边三角形
D. 若四边形![]() 是正方形,则
是正方形,则![]() 是等腰直角三角形
是等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解本校学生平均每天的课外做作业的时间情况,随机抽取部分学生进行问卷调查,并将调查的结果分为A、B、C、D四个等级(设做作业时间为t小时,A:t<1;B:1≤t<1.5;C:1.5≤t<2;D:t≥2)根据调查结果绘成了如下两幅不完整的统计图.
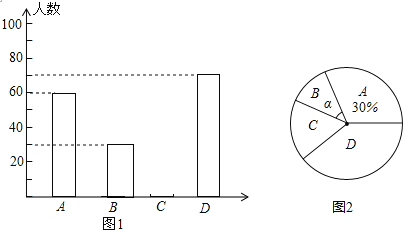
请根据图中信息,解答下列问题:
(1)本次调查中,抽取的学生人数是 ;
(2)图2中α的度数是 ,并补全图1条形统计图;
(3)该校共有2800名学生名,请估计作业时间不少于2小时的人数为 ;
(4)在此次调查中,甲班有2人平均每天的作业时间超过2小时,乙班有3名学生平均每天作业时间超过2小时,现从这5人中选取2人参加座谈会,请用树状图或列表的方法,求出“所选的2人来自不同班级”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com