
分析 利用配方法得到(x-2)2+(2y+1)2=0,根据非负数的性质得x-2=0,2y+1=0,然后解出x和y后代入$\frac{y}{{x}^{2}+{y}^{2}}$中计算即可.
解答 解:∵x2-4x+4+4y2+4y+1=0,
(x-2)2+(2y+1)2=0,
∴x-2=0,2y+1=0,解得x=2,y=-$\frac{1}{2}$,
∴$\frac{y}{{x}^{2}+{y}^{2}}$=$\frac{-\frac{1}{2}}{{2}^{2}+(-\frac{1}{2})^{2}}$=-$\frac{2}{17}$.
点评 本题考查了配方法的应用:利用配方法求二次三项式是一个完全平方式时所含字母系数的值.关键是:二次三项式是完全平方式,则常数项是一次项系数一半的平方.也考查了非负数的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
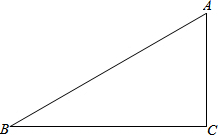 如图,在△ABC中,AB=17,BC=15,AC=8.
如图,在△ABC中,AB=17,BC=15,AC=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
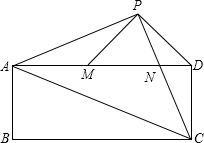 已知:如图,在矩形ABCD中,AC是对角线,点P为矩形外一点且满足AP=PC,AP⊥PC,PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
已知:如图,在矩形ABCD中,AC是对角线,点P为矩形外一点且满足AP=PC,AP⊥PC,PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com