Question

15．若平行四边形的一条边长是10，一条对角线长为8，则它的另一条对角线长x的取值范围是12＜x＜28．

Answer 1

分析 由平行四边形的性质得出OA=OC=$\frac{1}{2}$AC=4，OB=OD=$\frac{1}{2}$BD，在△BOC中，由三角形的三边关系定理得出OB的取值范围，得出BD的取值范围即可．

解答 解：如图所示：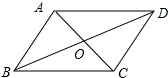
∵四边形ABCD是平行四边形，
∴OA=OC=$\frac{1}{2}$AC=4，OB=OD=$\frac{1}{2}$BD，
在△BOC中，BC=10，OC=4，
∴OB的取值范围是BC-OC＜OB＜BC+OC，
即6＜OB＜14，
∴BD的取值范围是12＜BD＜28．
故答案为：12＜x＜28．

点评 本题考查了平行四边形的性质、三角形的三边关系定理；熟练掌握平行四边形的性质和三角形的三边关系，并能进行推理计算是解决问题的关键．