
【题目】在一条不完整的数轴上从左到右有点![]() ,其中
,其中![]() ,
,![]() ,如图所示,设点
,如图所示,设点![]() 所对应数的和是
所对应数的和是![]() .
.
(1)若以![]() 为原点,则点
为原点,则点![]() 所对应的数是____,点
所对应的数是____,点![]() 所对应的数是_____,
所对应的数是_____,![]() ______.
______.
(2)若原点![]() 在图中数轴上点
在图中数轴上点![]() 的右边,且
的右边,且![]() ,求
,求![]() .
.
(3)若![]() , 求点
, 求点![]() 分别对应的数.
分别对应的数.
![]()
【答案】(1)-2,1,-1;(2)m=-22;(3)点A对应的数是-1,点B对应的数是1,点C对应的数是2.
【解析】
(1)由B是原点,根据两点间距离公式得出A、C所对应的数,求和,计算出m值即可;(2)有OC=6,根据两点间距离公式可求出C点对应的数,进而可得A、B两点对应的数,求和即可得m的值;(3)设A点对应的数为a,根据两点间距离可用a表示出B、C两点对应的数,由m=2,列方程即可求出a的值,即可得A点对应的数,进而可得B、C对应的数.
(1)∵B为原点,AB=2,BC=1,点A在B点左边,点C在B点右边,
∴A点对应的数是-2,C点对应的数是1,
∴m=-2+0+1=-1,
故答案为:-2,1,-1
(2)∵原点O在图中数轴上点![]() 的右边,且CO=6,
的右边,且CO=6,
∴C点对应的数是-6,
∵AB=2,BC=1,点A在B点左边,点B在C点左边,
∴B对应的数是-7,A对应的数是-9,
∴m=-9+(-7)+(-6)=-22.
(3)设A点对应的数为a,
∵AB=2,BC=1,点B在A点右边,点C在B点右边,
∴点B对应的数是a+2,点C对应的数是a+2+1=a+3,
∵m=2,
∴a+a+2+a+3=2,
解得:a=-1,
∴点A对应的数是-1,
∴点B对应的数是1,点C对应的数是2.


科目:初中数学 来源: 题型:
【题目】填空:
(1)一元二次方程的一般式是 __________.
(2)把一元二次方程![]() 化成一般式是__________.
化成一般式是__________.
(3)把一元二次方程![]() 化成一般式是__________.
化成一般式是__________.
(4)一元二次方程![]() 的二次项的系数是__________,一次项的系数是__________, 常数项是__________.
的二次项的系数是__________,一次项的系数是__________, 常数项是__________.
(5)一元二次方程![]() 的二次项的系数是_______,一次项的系数是_______,常数项是_______.
的二次项的系数是_______,一次项的系数是_______,常数项是_______.
(6)当![]() __________ 时,关于
__________ 时,关于![]() 的方程
的方程![]() 是一元二次方程.
是一元二次方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学实验室:
![]()
我们知道,在数轴上,|a|表示数a的点到原点的距离,这是绝对值的几何意义.进一步地,数轴上的两个点A、B,分别表示有理数a、b,那么A、B两点之间的距离AB=|a-b|.利用此结论,回答以下问题:
(1)数轴上表示1和5的两点之间的距离是______,数轴上表示1和-5的两点之间的距离是______.(1+1分,注意写出最后结果)
(2)式子|x+2|可以看做数轴上表示x和______的两点之间的距离.
(3)式子|x+2|+|x-3|的最小值是______.
(4)当|x+2|+|x-3|取得最小值时,数x的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:
(1)填空:甲种收费的函数表达式是 ,乙种收费的函数表达式是 .
(2)请你根据不同的印刷数量帮忙确定选择哪种印刷方式较合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
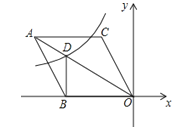
【题目】如图,已知抛物线y=﹣![]() +bx+c图象经过A(﹣1,0),B(4,0)两点.
+bx+c图象经过A(﹣1,0),B(4,0)两点.
(1)求抛物线的解析式;
(2)若C(m,m﹣1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②连结EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:对于排好顺序的三个数:![]() 称为数列
称为数列![]() .将这个数列如下式进行计算:
.将这个数列如下式进行计算: ![]() ,
,![]() ,
,![]() ,所得的三个新数中,最大的那个数称为数列
,所得的三个新数中,最大的那个数称为数列![]() 的“关联数值”.
的“关联数值”.
例如:对于数列![]() 因为
因为![]()
![]()
![]() 所以数列
所以数列![]() 的“关联数值”为6.进一步发现:当改变这三个数的顺序时,所得的数列都可以按照上述方法求出“关联数值”,如:数列
的“关联数值”为6.进一步发现:当改变这三个数的顺序时,所得的数列都可以按照上述方法求出“关联数值”,如:数列![]() 的 “关联数值”为0;数列
的 “关联数值”为0;数列![]() 的“关联数值”为3...而对于“
的“关联数值”为3...而对于“![]() ”这三个数,按照不同的排列顺序得到的不同数列中,“关联数值"的最大值为6.
”这三个数,按照不同的排列顺序得到的不同数列中,“关联数值"的最大值为6.
(1)数列![]() 的“关联数值”为_______;
的“关联数值”为_______;
(2)将“![]() ”这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值是_______, 取得“关联数值”的最大值的数列是______
”这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值是_______, 取得“关联数值”的最大值的数列是______
(3)将“![]() ”
”![]() 这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值为10,求
这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值为10,求![]() 的值,并写出取得“关联数值”最大值的数列.
的值,并写出取得“关联数值”最大值的数列.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,![]() ),反比例函数
),反比例函数![]() 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
A. ![]() B. -
B. -![]() C.
C. ![]() D. -
D. -![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在数轴上A点表示数![]() ,B点表示数
,B点表示数![]() ,
,![]() 、
、![]() 满足|
满足|![]() |+|
|+|![]() |=0;
|=0;
![]()
(1)点A表示的数为_____;点B表示的数为_____;
(2)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
①当t=1时,甲小球到原点的距离=_____;乙小球到原点的距离=_____.
当t=3时,甲小球到原点的距离=_____;乙小球到原点的距离=_____.
②试探究:甲,乙两小球到原点的距离可能相等吗?若不能,请说明理由.若能,请直接写出甲,乙两小球到原点的距离相等时经历的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com