
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,把矩形沿
,把矩形沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,当
处,当![]() 为直角三角形时,
为直角三角形时,![]() 的长为_____.
的长为_____.

【答案】6或3
【解析】
当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如答图1所示.
连结AC,先利用勾股定理计算出AC=10,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=6,可计算出CB′=4,设BE=x,则EB′=x,CE=8-x,然后在Rt△CEB′中运用勾股定理可计算出x.
②当点B′落在AD边上时,如答图2所示.此时四边形ABEB′为正方形.
解:当△CEB′为直角三角形时,有两种情况: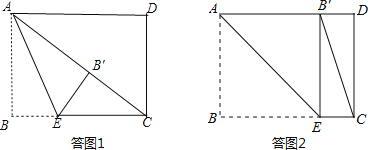
①当点B′落在矩形内部时,如答图1所示.
连结AC,
在Rt△ABC中,AB=6,BC=8,
∴AC=![]() =10,
=10,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,如图,
∴EB=EB′,AB=AB′=6,
∴CB′=10-6=4,
设BE=x,则EB′=x,CE=8-x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2,
∴x2+42=(8-x)2,
解得x=3,
∴B′E=3;
②当点B′落在AD边上时,如答图2所示.
此时ABEB′为正方形,
∴BE=AB=6.
综上所述,B′E的长为3或6.
故答案为:6或3.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料
小白遇到这样一个问题:
如图,点C是段AB的中点,AD=![]() DB,CD=10,求AB的长.
DB,CD=10,求AB的长.
![]()
小白的思路是:设AB=x,根据“CD=10“列方程,请按照小白的思路完成此问题的解答
用学过的知识或参考小白的方法,解决下面的问题:
已知OC、OD是∠AOB的内部的两条射线,∠AOC═![]() ∠AOB,∠AOD=m∠DOB,∠COD=n(m、n为常数,且m≠
∠AOB,∠AOD=m∠DOB,∠COD=n(m、n为常数,且m≠![]() )
)
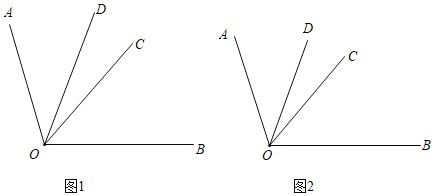
(1)如图1,若m=![]() ,n=22,求∠DOB的度数.
,n=22,求∠DOB的度数.
(2)如图2,若n=14(3﹣2m)求∠DOB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机械厂甲、乙两个生产车间承担生产同一种零件的任务,甲、乙两车间共有50人,甲车间平均每人每天生产零件30个.乙车间平均每人每天生产零件20个,甲车间每天生产零件总数与乙车间每天生产零件总数之和为1300个.
(1)求甲、乙两车间各有多少人?
(2)该机械厂改进了生产技术。在甲、乙两车间总人数不变的情况下,从甲车间调出一部分人到乙车间.调整后甲、乙两车间平均每人每天生产零件都比原来多5个,甲乙两车间每天生产零件总数之和是1480个,且甲、乙两车间每人的计件工资(按完成件数发放工资)分别是12元和9元,求甲、乙两车间每天计件收入总和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°, ∠B=30°,BC=![]() +1,点E、F分别是BC、AC边上的动点,沿EF所在直线折叠∠C,使点C的对应点C′始终落在边AB上,若△BEC′是直角三角形时,则BC′的长为_____________.
+1,点E、F分别是BC、AC边上的动点,沿EF所在直线折叠∠C,使点C的对应点C′始终落在边AB上,若△BEC′是直角三角形时,则BC′的长为_____________.
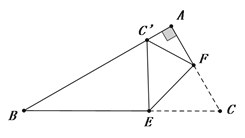
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元9世纪,阿拉伯数学家阿尔花拉子米在他的名著《代数学》中用图解一元二次方程,他把一元二次方程![]() 写成
写成![]() 的形式,并将方程左边的
的形式,并将方程左边的![]() 看作是由一个正方形(边长为
看作是由一个正方形(边长为![]() )和两个同样的矩形(一边长为
)和两个同样的矩形(一边长为![]() ,另一边长为
,另一边长为![]() )构成的矩尺形,它的面积为
)构成的矩尺形,它的面积为![]() ,如图所示。于是只要在这个图形上添加一个小正方形,即可得到一个完整的大正方形,这个大正方形的面积可以表小为:
,如图所示。于是只要在这个图形上添加一个小正方形,即可得到一个完整的大正方形,这个大正方形的面积可以表小为:![]() ____
____![]() _______ ,整理,得
_______ ,整理,得![]() ,因为
,因为![]() 表示边长,所以
表示边长,所以![]() ___________.
___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1:在等边△ABC中,点D,E分别在边AB,AC上,AD=AE,连结BE,CD,点M、N、P分别是BE、CD、BC的中点.
(1)观察猜想
图1中△PMN的形状是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,△PMN的形状是否发生改变?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点![]() ,其中
,其中![]() ,
,![]() ,如图所示,设点
,如图所示,设点![]() 所对应数的和是
所对应数的和是![]() .
.
(1)若以![]() 为原点,则点
为原点,则点![]() 所对应的数是____,点
所对应的数是____,点![]() 所对应的数是_____,
所对应的数是_____,![]() ______.
______.
(2)若原点![]() 在图中数轴上点
在图中数轴上点![]() 的右边,且
的右边,且![]() ,求
,求![]() .
.
(3)若![]() , 求点
, 求点![]() 分别对应的数.
分别对应的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com