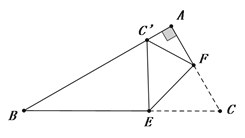
【题目】如图，在Rt△ABC中，∠A＝90°, ∠B＝30°，BC＝
＋1，点E、F分别是BC、AC边上的动点，沿EF所在直线折叠∠C，使点C的对应点C′始终落在边AB上，若△BEC′是直角三角形时，则BC′的长为_____________．
【答案】
或2
【解析】分析：分两种情况：①当∠BEC′=90°时，设EC′=x，则BE=
x，BC′=2x，EC=x，由BC=BE+EC，可求出x的值，即可得到结论；
②当∠BC′E=90°时，设EC′=x，则BE=2x，BC′=x，EC=x，由BC=BE+EC，可求出x的值，即可得到结论．
详解：分两种情况：①当∠BEC′=90°时，设EC′=x，则BE=x，BC′=2x，EC=x，∴BC=BE+EC=x+x=+1，解得：x=1，∴BC′=2x=2；
②当∠BC′E=90°时，设EC′=x，则BE=2x，BC′=x，EC=x，∴BC=BE+EC=2x+x=+1，解得：x=
，∴BC′=x=．
故答案为：或2．
科目：初中数学 来源： 题型：
【题目】列方程解决下列问题
一艘船从甲码头到乙码头顺流而行，用了2小时；从乙码头返回甲码头逆流而行，用了2.5小时，已知水流的速度为3千米/时．
（1）求船在静水中的平均速度；
（2）求甲，乙两个码头之间的路程．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】填空：
（1）一元二次方程的一般式是 __________．
（2）把一元二次方程
化成一般式是__________．
（3）把一元二次方程
化成一般式是__________．
（4）一元二次方程
的二次项的系数是__________，一次项的系数是__________， 常数项是__________．
（5）一元二次方程
的二次项的系数是_______，一次项的系数是_______，常数项是_______．
（6）当
__________ 时，关于
的方程
是一元二次方程．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】光华中学库存若干套桌椅，准备修理后支援贫困山区学校.现有甲、乙两修理组，甲修理组单独完成任务需要12天，乙修理组单独完成任务需要24天.
（1）若由甲、乙两修理组同时修理，需多少天可以修好这些套桌椅？
（2）若甲、乙两修理组合作3天后，甲修理组因新任务离开,乙修理组继续工作.甲完 成新任务后，回库与乙又合作3天，恰好完成任务.问：甲修理组离开几天？
（3）学校需要每天支付甲修理组、乙修理组修理费分别为80元，120元.任务完成后， 两修理组收到的总费用为1920元，求甲修理组修理了几天？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB为半圆O的直径，C为AO的中点，CD⊥AB交半圆于点D，以C为圆心，CD为半径画弧交AB于E点，若AB＝4，则图中阴影部分的面积是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把下列各数填在相应的集合里：
…
正分数集合：｛_____________________…｝负有理数集合：｛____________________…｝
无理数集合：｛_____________________…｝非负整数集合：｛____________________…｝
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】数学实验室：
我们知道，在数轴上，|a|表示数a的点到原点的距离，这是绝对值的几何意义.进一步地，数轴上的两个点A、B，分别表示有理数a、b，那么A、B两点之间的距离AB=|a－b|.利用此结论，回答以下问题：
（1）数轴上表示1和5的两点之间的距离是______，数轴上表示1和－5的两点之间的距离是______.（1+1分，注意写出最后结果）
（2）式子|x+2|可以看做数轴上表示x和______的两点之间的距离.
（3）式子|x+2|＋|x－3|的最小值是______.
（4）当|x+2|＋|x－3|取得最小值时，数x的取值范围是______.
查看答案和解析>>
科目：初中数学 来源： 题型：
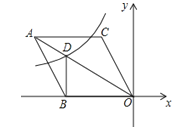
【题目】如图，在平面直角坐标系中，菱形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，∠BOC=60°，顶点C的坐标为（m，
），反比例函数
的图像与菱形对角线AO交于D点，连接BD，当BD⊥x轴时，k的值是（ ）
A. 
B. － C. 
D. －
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
