【题目】列方程解决下列问题
一艘船从甲码头到乙码头顺流而行，用了2小时；从乙码头返回甲码头逆流而行，用了2.5小时，已知水流的速度为3千米/时．
（1）求船在静水中的平均速度；
（2）求甲，乙两个码头之间的路程．
科目：初中数学 来源： 题型：
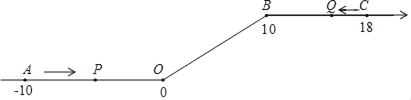
【题目】如图，将一条数轴在原点O和点B处各折一下，得到一条“折线数轴”．图中点A表示﹣10，点B表示10，点C表示18，我们称点A和点C在数轴上相距28个长度单位，动点P从点A出发，以2单位/秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半；点P从点A出发的同时，点Q从点C出发，以1单位/秒的速度沿着“折线数轴”的负方向运动，当点P到达B点时，点P、Q均停止运动．设运动的时间为t秒．问：
（1）用含t的代数式表示动点P在运动过程中距O点的距离；
（2）P、Q两点相遇时，求出相遇时间及相遇点M所对应的数是多少？
（3）是否存在P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等时？若存在，请直接写出t的取值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知ab＜0，
，且|c|＞|b|＞|a|，数轴上a、b、c对应的点是A、B、C.
(1) 若|a|＝－a时，请在数轴上标出A、B、C的大致位置；
(2) 在(1)的条件下，化简：|a－b|－|b＋c|＋|c＋a|.
查看答案和解析>>
科目：初中数学 来源： 题型：
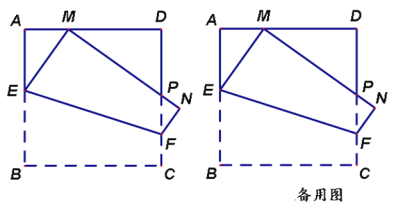
【题目】如图，在边长为1的正方形ABCD中，动点E，F分别在边AB，CD上，将正方形ABCD沿直线EF折叠，使点B的对应点M始终落在边AD上（点M不与点A，D重合），点C落在点N处，MN与CD交于点P，设BE=x。
（1）当AM=
时，求x的值；
（2）随着点M在边AD上位置的变化，ΔPDM的周长是否发生变化？如变化，请说明理由；如不变，请求出该定值；
（3）若AM=a,四边形BEFC的面积为S，求S与a之间的函数表达式。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，点E，F在对角线AC上，且AE=CF。
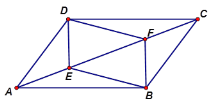
（1）求证：四边形DEBF是平行四边形；
（2）若DE=3，CD=4，∠EDC=90°，当四边形DEBF是菱形时，AE的长为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列各组依次排列的数，它的排列有什么规律？你能按此规律写出第2008个数?⑴ 1，2，－3，－4，5，6，－7，－8，…，________（第2008个数），…⑵ 1，
，
，
，
，
，
，
，…，________（第2008个数），…
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料
小白遇到这样一个问题：
如图，点C是段AB的中点，AD＝
DB，CD＝10，求AB的长．
小白的思路是：设AB＝x，根据“CD＝10“列方程，请按照小白的思路完成此问题的解答
用学过的知识或参考小白的方法，解决下面的问题：
已知OC、OD是∠AOB的内部的两条射线，∠AOC═
∠AOB，∠AOD＝m∠DOB，∠COD＝n（m、n为常数，且m≠
）
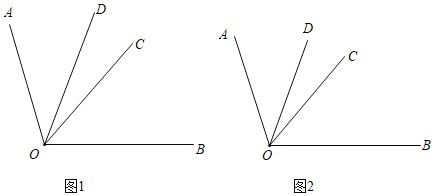
（1）如图1，若m＝，n＝22，求∠DOB的度数．
（2）如图2，若n＝14（3﹣2m）求∠DOB的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
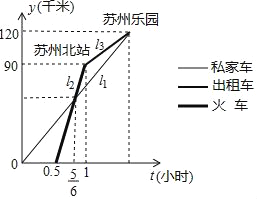
【题目】“五一”期间小明和小丽相约到苏州乐园游玩，小丽乘私家车从上海出发30分钟后，小明乘坐火车从上海出发，先到苏州北站，然后再乘出租车去游乐园（换乘时间忽略不计），两人恰好同时到达苏州乐园，他们离上海的距离y（千米）与乘车时间t（小时）的关系如图所示，请结合图象信息解决下面问题：
（1）本次火车的平均速度_________千米/小时？
（2）当小明到达苏州北站时，小丽离苏州乐园的距离还有多少千米？
查看答案和解析>>
科目：初中数学 来源： 题型：
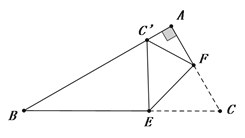
【题目】如图，在Rt△ABC中，∠A＝90°, ∠B＝30°，BC＝
＋1，点E、F分别是BC、AC边上的动点，沿EF所在直线折叠∠C，使点C的对应点C′始终落在边AB上，若△BEC′是直角三角形时，则BC′的长为_____________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
