
科目:初中数学 来源: 题型:选择题
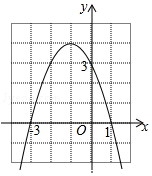 如图是二次函数y=ax2+bx+c的图象,下列结论错误的是( )
如图是二次函数y=ax2+bx+c的图象,下列结论错误的是( )| A. | 二次函数y=ax2+bx+c的最大值为4 | |
| B. | 常数项c为3 | |
| C. | 一元二次方程ax2+bx+c=0的两根之和为-2 | |
| D. | 使y≤3成立的x的取值范围是x≥0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
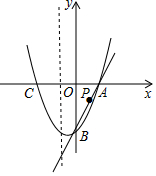 如图,直线y=3x-6与x轴相交于点A,与y轴相交于点B,抛物线y=x2+bx+c过点A、B两点,该抛物线与x轴的另一个交点为C.
如图,直线y=3x-6与x轴相交于点A,与y轴相交于点B,抛物线y=x2+bx+c过点A、B两点,该抛物线与x轴的另一个交点为C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC是等边三角形,BC=4,以B点为原点,BC所在的直线为x轴,建立直角坐标系,则A点的坐标为(2,2$\sqrt{3}$).
如图,△ABC是等边三角形,BC=4,以B点为原点,BC所在的直线为x轴,建立直角坐标系,则A点的坐标为(2,2$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在一块边长为a的正方形花圃中,两纵两横的4条宽度为b的人行道把花圃分成9块,下面是四个计算种花土地总面积的代数式:①(a-2b)(a-2b),②a2-4ab,③a2-4ab-4b2,④a2-4ab+4b2,其中正确的有( )
如图,在一块边长为a的正方形花圃中,两纵两横的4条宽度为b的人行道把花圃分成9块,下面是四个计算种花土地总面积的代数式:①(a-2b)(a-2b),②a2-4ab,③a2-4ab-4b2,④a2-4ab+4b2,其中正确的有( )| A. | ② | B. | ①③ | C. | ①④ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对于每一个确定的x的值,y都有唯一确定的值与它相对应 | |
| B. | 只要任意给出一个x的值,就能确定y的值,所以此方程的解为任何实数 | |
| C. | 若需满足x、y都为正整数,则此方程恰有两个解 | |
| D. | 它可与二元一次方程5x-3z=2组成一个二元一次方程组 |
查看答案和解析>>
科目:初中数学 来源:2017届浙江省九年级3月模拟数学试卷(解析版) 题型:解答题
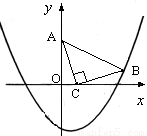
如图,在直角坐标系中,已知点A(0, 3)、点C(1, 0),等腰Rt△ACB的顶点B在抛物线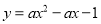 上.
上.
(1)求点B的坐标及抛物线的解析式;
(2)在抛物线上是否存在点P(点B除外),使△ACP是以AC为直角边的Rt△?若存在,求出所有点P的坐标;若不存在,请说明理由.
(3)在抛物线上是否存在点Q(点B除外),使△ACQ是以AC为直角边的等腰Rt△?若存在直接写出所有点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳市九年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列命题正确的是( )
①三角形中最大内角一定不小于600;
② 所有等腰直角三角形都相似;
③正多边形的外角为240,则它的中心角也为240;
④顺次连接对角线相等的四边形各边中点得到矩形.
A. ①② B. ①②③ C. ②③④ D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com