练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．设A、B、C三点依次分别是抛物线y=x2-4x-5与y轴的交点以及与x轴的两个交点，则△ABC的面积是15．

    分析 分别求出抛物线与y轴的交点A和与x轴的交点B、C的坐标，得到线段BC的长，根据三角形面积公式求出面积即可．

    解答 解：当x=0时，y=-5，点A的坐标（0，-5），
    当y=0时，x2-4x-5=0，解得x1=-1，x2=5，
    点B的坐标（-1，0），点C的坐标（5，0），则BC=6，
    △ABC的面积为：$\frac{1}{2}$×6×5=15．

    点评 本题考查的是抛物线与x轴的交点的求法，理解抛物线与x轴的交点的横坐标与一元二次方程的根的关系是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

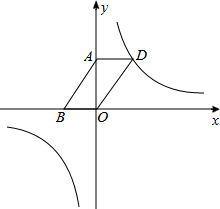    10．已知反比例函数$y=\frac{m-1}{x}$（m为常数）的图象在第一、三象限内．
    （1）求m的取值范围；
    （2）如图，若该反比例函数的图象经过平行四边形ABOD的顶点D，点A、B的坐标分别为（0，3），（-2，0）．
    ①求出该反比例函数解析式；
    ②设点P是该反比例函数图象上的一点，且在△DOP中，OD=OP，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．计算：${（\sqrt{2}）^{-1}}$=$\frac{\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．分解因式：2x2-8x=2x（x-4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，线段AB是圆O的直径，弦CD⊥AB，如果∠BOC=70°，那么∠BAD等于（　　）
    A．20°B．30°C．35°D．70°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．不等式组的解集在数轴上表示如图，则该不等式组是（　　）
    A．$\left\{\begin{array}{l}x≥-1\\ x≤2\end{array}\right.$B．$\left\{\begin{array}{l}x＜-1\\ x≥2\end{array}\right.$C．$\left\{\begin{array}{l}x＞-1\\ x＜2\end{array}\right.$D．$\left\{\begin{array}{l}x＞-1\\ x≤2\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

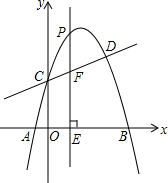    12．如图，抛物线y=ax2+$\frac{7}{2}$x+c与直线y=kx+2交于C，D两点，其中点C在y轴上，点D的坐标为（3，$\frac{7}{2}$）．点P是y轴右侧的抛物线上一动点，过点P作PE⊥x轴于点E，交CD于点F．
    （1）求直线和抛物线的解析式；
    （2）若点P的横坐标为m，当m为何值时，以O，C，P，F为顶点的四边形是平行四边形？请说明理由．
    （3）是否存在点P，使∠PCF=45°？若存在，请求出相应的点P的坐标；若不存在请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

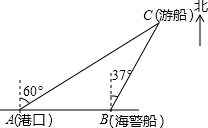    9．一艘观光游船从港口A处以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号．一艘在港口正东方向B处的海警船接到求救信号，测得事故船在它的北偏东37°方向．
    （1）求海警船距离事故船C的距离BC．
    （2）若海警船以40海里/小时的速度前往救援，求海警船到达事故船C处大约所需的时间．（温馨提示：sin53°≈0.8，cos53°≈0.6）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．将点A（-3，-2）向左平移5个单位，再向下平移4个单位得到点B，则点B的坐标为（　　）
    A．（-8，2）B．（-8，-6）C．（2，-2）D．（2，2）

    查看答案和解析>>

    同步练习册答案